5

Sampling with replacement $N$ items from $K$, where $N \geq K$, what is the probability that each item in $K$ is selected at least once?

For example, from $10,000$ individuals, what is the probability that every birthday is represented? (assume each birthday $p = 1/365$)

I've been using simulations to work this out, but would like to know the general solution. Thanks!

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
not_my_birthday
  • 51
  • 1
  • 2
  • 2
    This is a duplicate question on this site and probably also on math.SE. Please use the search facilities to locate it. Cheers and welcome to the site. – cardinal Jun 14 '12 at 21:23
  • This may be a difficult search, @cardinal. Given that the solution is best expressed in terms of Stirling numbers, I [searched for such threads](http://stats.stackexchange.com/search?q=%2Bstirling), to no avail. Did you have a particular set of keywords in mind? – whuber Jun 14 '12 at 22:17
  • I took down my answer because I saw the flaw in the argument. This is what I wrote before I took it down. My mistake here is that I was thinking that if I don't fill the designated k slots with one of each type I can't get all k in the N slots. But that is not true because the missing type(s) could still be in the remaining N-k slots. So this argument does not work at all and I took down my answer. – Michael R. Chernick Jun 14 '12 at 22:55
  • @whuber, as you know, this is just the [coupon collector problem](http://en.wikipedia.org/wiki/Coupon_collector%27s_problem) and is closely related to the [birthday problem](http://en.wikipedia.org/wiki/Birthday_problem). Several links to math.SE and stats.SE questions to follow. – cardinal Jun 14 '12 at 23:10
  • 2
    Duplicates and related questions: (**1**) [Birthday-coverage problem](http://math.stackexchange.com/questions/26772) (*duplicate*), (**2**) [What is a tight lower bound on the coupon collector time?](http://stats.stackexchange.com/questions/7774) (*related*), (**3**) [Probability of 3 people in a room of 30 having the same birthday](http://math.stackexchange.com/questions/25876) (*related*), (**4**) [A Question About Dice](http://math.stackexchange.com/questions/25568) (*related*), (**5**) [Probability of at least one unique outcome](http://stats.stackexchange.com/questions/6762) (*related*). – cardinal Jun 14 '12 at 23:18
  • 1
    There are lots more on the both problems and many variants. Searching with `+coupon` or `+birthday` on both sites is relatively fruitful. – cardinal Jun 14 '12 at 23:18
  • Didn't realise it's called the coupon collector problem. Thanks @cardinal. – not_my_birthday Jun 14 '12 at 23:54
  • 4
    @not_my_birthday: You're welcome! Welcome to the site! :) Your question is an interesting one, but also a well-known one. Please don't be discouraged by the suggestion to look for duplicates. I hope you'll look around and continue to participate here. Cheers. :) – cardinal Jun 15 '12 at 01:50
  • @cardinal This raises an interesting issue: yes, the question is *almost* duplicated on the math site: it asks the inverse question (find $k$ in terms of the probability). It has correct answers there and even presents some supplementary ideas on asymptotics. However, the answers are unilluminating--they have no explanation of the result--and one has to read through them all, down to the lowest-voted one, to find any reference. I am thinking it may be useful to keep our question open, provided it gets an answer with a statistical rather than a mathematical focus. – whuber Jun 15 '12 at 12:34
  • @whuber: I'm sorry you found our answers unilluminating; they do tend to be more terse over there. (Mine did have a reference buried in there, by the way.) To me, the ultimate reference is knowing what to call a famous problem. That usually unlocks a wealth of available resources to explore. I agree that having an answer with a bit different viewpoint might be fruitful – cardinal Jun 15 '12 at 13:07
  • @whuber: By the way, were you offering your services toward this end? Perhaps another Pooh adventure... – cardinal Jun 15 '12 at 13:09
  • @cardinal I didn't notice one of the replies was yours :-). I should have more tactfully indicated that "unilluminating" referred to the relevance of those replies to the *present* question here on stats, not the (different) question as posed on math. I agree about the value of knowing how to look something up. That's the "interesting issue" I had in mind: it may be useful to have some threads here that duplicate those on math (or elsewhere on SE) *because they can be found through appropriate searches here.* – whuber Jun 15 '12 at 13:11
  • @cardinal This one doesn't need a Pooh approach, thank you! But in light of the difficulties experienced in the withdrawn reply to this thread, it seems that it would be good to provide some explanation of the combinatorial reasoning that produces the correct answer, rather than just a formula. – whuber Jun 15 '12 at 13:14
  • @whuber: I am just teasing a bit. I was not the least bit offended. :) – cardinal Jun 15 '12 at 13:14
  • @whuber: By the way, I included that question as a *duplicate* more for the answers than for the question itself. I would argue that both Byron's and my own are *directly relevant* since they respond directly to *this* question and a bit more *indirectly* to the question posed on math.SE. :-) – cardinal Jun 15 '12 at 13:20

1 Answers1

5

For completeness's sake, here's an answer and some references.

Because each sample has equal probability, it suffices to count the number of samples with the desired property and divide by the total number of samples.

  1. Let's tackle the denominator first, because it's easier to count. A "sample" can be uniquely described by the sequence of results. Abstractly, that's a function $s$ from $\{1,2,\ldots,N\}$ to the set of items or, equivalently, an $N$-vector with coefficients in a set of $K$ things. Because there are $K$ ways to specify each coefficient, the total number of samples equals $K^N$.

  2. The numerator is the number of samples in which each item appears at least once. In mathematical terminology, $s$ is a surjection (or "onto" function). Combinatorics texts explain how to count surjections and they provide formulas. For instance, Wagner's Basic Combinatorics covers this on the first page of Chapter 9 and the first page of Chapter 10. The upshot is that the numerator equals $K!$ times the Stirling number of the second kind, $S(N,K)$.

The desired probability therefore equals $K! S(N,K) /K^N$.

This technique of first reducing a probability to a counting problem and then expressing that counting problem in terms of a set of functions with specific properties gives a general method for characterizing problems of this type. (Gian-Carlo Rota's Twelvefold Way provides a unified approach to such problems.) With such a characterization in hand you can often then look up the answer.

As an example of this particular formula, consider the case $K=2$ and $N=4$. We can look up or compute that $S(N,K)=7$, whence the probability is $2! \times 7 / 2^4$ = $14/16$. We can check by enumerating all samples of size $4$ from a set of $2$ items, such as $\{A,B\}$:

$AAAA, AAAB, AABA, AABB, ABAA, ABAB, ABBA, ABBB, BAAA, BAAB, BABA, BABB, BBAA, BBAB, BBBA, BBBB.$

Of these, the first and last omit one of the items but the remaining $14$ out of the $16$ samples include both.

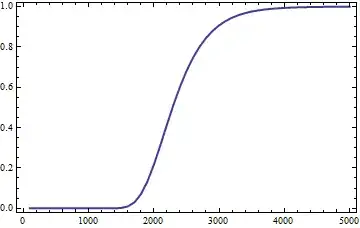
Finally, the question asks for the answer when $N=10^4$ and $K=365$. It differs from $1$ by $4.44104 \times 10^{-10}$. It is interesting to see how this probability depends on $N$ (keeping $K$ fixed at $365$):

Plot of probabilities vs. N

whuber
  • 281,159
  • 54
  • 637
  • 1,101