Hi all,
I need some advice on possible algorithms that I can apply to the following problem (if possible with pointers to implementations of these algorithms).
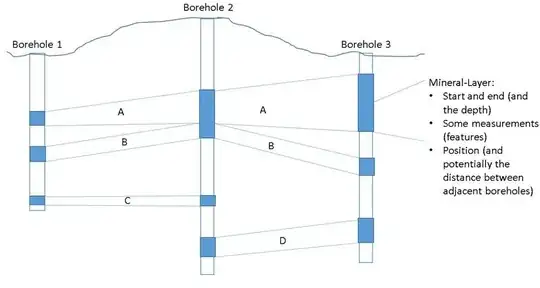
The dataset: I have some dataset about boreholes drilled in the earth. For each of the boreholes we know that there are some intervals which contain a certain mineral that we would like to mine (see the blue squares above).
- A start end end point of the interval.
- Some measurements (mainly continuous features)
The task:
- Predict the mapping between different mineral-layers of different boreholes. In other words: Predict that the first interval in Borehole1 and Borehole 3 belongs to layer ‘A’. The first interval in Borehole 2 is split up and the first one belongs to “A” (that name “A” is arbitrary and can be any category.
- Supervised training data is available (presumably not enough for big neural networks).
The specific properties of the problem:
- Intervals must not cross. So interval A might never continue below interval B.
- Intervals might stop. Interval “C” does e.g. not continue in Borehole 3.
- One borehole might have multiple intervals that are mapped to one mineral layer (not in the graphic!!!) So for example the large blue A layer in borehole 3 might occur in 3 subsequent intervals.
My question:
Which machine learning algorithm could I use. Or more specifically:
- Which algorithm allows to specify constraints on the predicted value (like that intervals must not cross)?
I am keeping that question pretty open on purpose since I would like to keep my mind open to new ideas from you guys!
Thanks for any help.