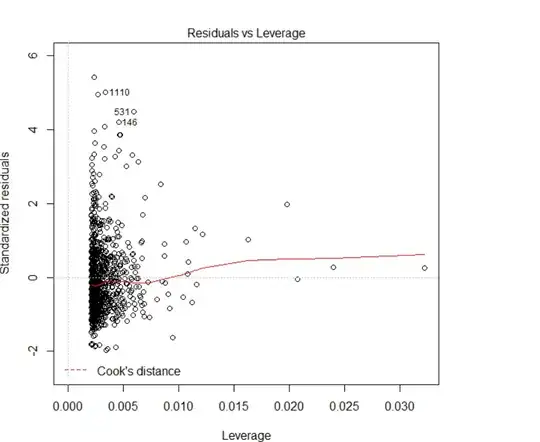
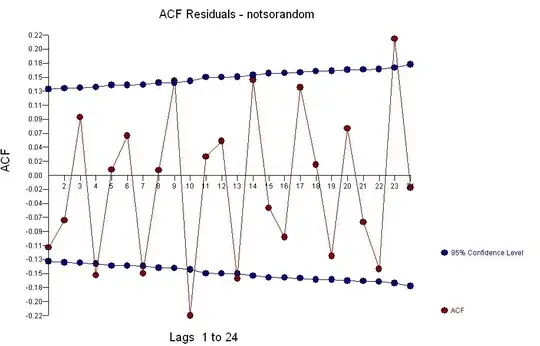
I have a continuous dependent which is the concentration in the blood and several independent variables. I applied the linear regression and it seems that there is the violation of assumption.The R square of the model is 0.06. We have enough sample size around 900 observations but I was wondering if it is reasonable to apply linear regression in this example? I also took log of the dependent variable but again it seems we have the violation of the assumption especially linearity. Am I right? The dependent variable is very skew. Do you recommend using quantile regression or running the regression on the dependent variable If you believe the model is linear?
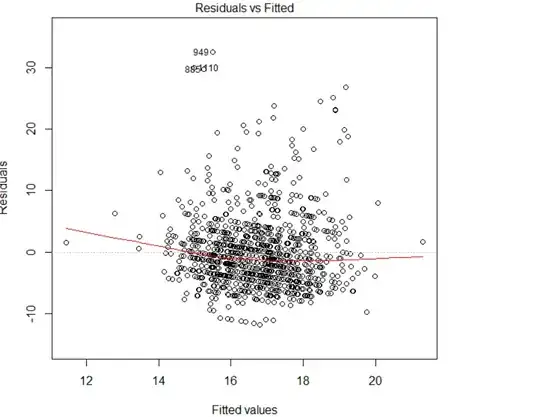
Here is the plot of residuals vs fitted values after taking log.