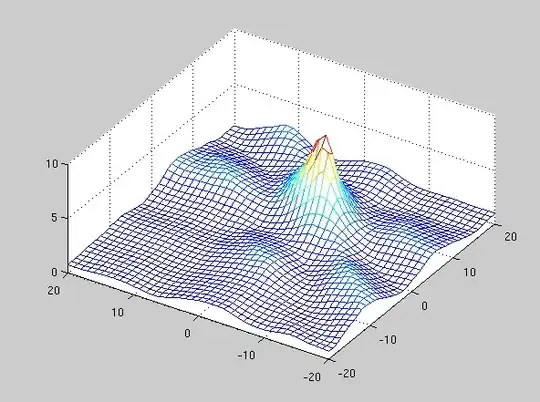
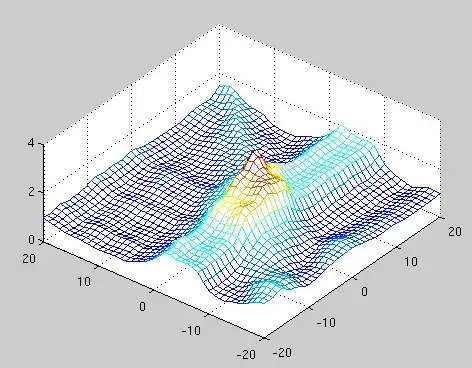
I've got an optimization problem with these properties:
- The goal function is not cheap to compute. It can be evaluated up to around 10^4 times in the optimization.
- There's a lot of local optima.
- High values are clustered around the maximum, so the problem is kind of convex.
- The solutions are constrained to a known hyperbox.
- The gradient is unknown, but intuitively, the function is smooth.
- It's a function of up to 50 variables. The graphs below are examples of the 2D special case.
Nelder-Mead gets stuck in the local optima a lot. Above three variables, there's no chance of using brute force. I've looked into genetic algorithms, but they seem to require a lot of evaluations of the goal function.
What kind of algorithm should I be looking for?