9

When implementing dropout (or drop connect) - do you need to account for the case that every node in a layer is dropped?

Even though this is a very small chance, what is the correct approach to take in this scenario? Pick a new random set to drop out or set all the inputs to the next layer to be zero?

Does anyone know what the popular libraries (TensorFlow, Keras, etc.) do in this situation?

Dan
  • 1,288
  • 2
  • 12
  • 30
  • 1
    This is a real issue despite what some answers say. I'm working with networks that have a very small number of neurons in a layer and dropout causes the model to start outputting NAN for any input in Keras. – Frobot Nov 11 '21 at 00:05

2 Answers2

5

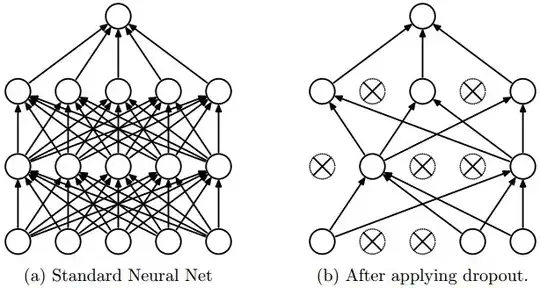
This is a concern which will very rarely every be realized. For a moderately sized neural network whose hidden layers each have $1000$ units, if the dropout probability is set to $p=0.5$ (the high end of what's typically used) then the probability of all $1000$ units being zero is $0.5^{1000} = 9.3\times10^{-302}$ which is a mind-bogglingly tiny value. Even for a very small neural network with only $50$ units in the hidden layer, the probability of all units being zero is $.5^{50}=8.9\times10^{-16}$, or less than $\frac{1}{1\ \text{thousand trillion}}$

So in short, this isn't something you ever need to worry about in most real-world situations, and in the rare instances where it does happen, you could simply rerun the dropout step to obtain a new set of dropped weights.

UPDATE:

Digging through the source code for TensorFlow, I found the implementation of dropout here. TensorFlow doesn't even bother accounting for the special case where all of the units are zero. If this happens to occur, then the output from that layer will simply be zero. The units don't "disappear" when dropped, they just take on the value zero, which from the perspective of the other layers in the network is perfectly fine. They can perform their subsequent operations on a vector of zeros just as well as on a vector of non-zero values.

jon_simon
  • 1,679
  • 1
  • 14
  • 26
  • For realistic problems it is extremely unlikely, however with most libraries there is nothing stopping me from making a 2 node layer which would have a very high probability of dropping all the nodes. So I'm interested to know how the major implementations have accounted for this or if you have any references backing up the suggestion to just pick again (which is what I would guess is the best action as well) – Dan Sep 12 '17 at 00:19
  • 1
    @Dan See my updated response – jon_simon Sep 12 '17 at 02:32
0

That situation should be avoided. If all the neurons in one of the hidden layers are dropped, signals would not proceed towards the output neuron, and your neural network would not function as wanted. As you could see in below picture, only a part of your neurons in a layer are dropped.

enter image description here

You normally set the dropout rates for each hidden layer. So, if you set the dropout rates below 1, that sort of situation is avoided.

Below is how dropout layer is implemented in Tensorflow and Keras. You generally set the dropout rates for all the hidden layers as the same number (0.x) as it is convenient to tune the hyperparameter. 

# set the dropout rate as any number between 0 and 1
dropout_rate = 0.4

# tensorflow implementation
dropout = tf.nn.dropout(x, keep_prob = dropout_rate)

# keras implementation
dropout = keras.layers.Dropout(dropout_rate)
Buomsoo Kim
  • 420
  • 2
  • 4
  • 3
    No, setting the dropout rate below 1 does not guarantee that the situation will be avoided. For an extreme example, consider a drop-rate of 0.9 and in a hidden layer having 10 units. Then the probability that all units are dropped = 0.9^10 = .349, or in order words more than a third of the time. – jon_simon Sep 11 '17 at 03:08
  • @jon_simon Yes, I did not consider such extreme situation. But my conjecture was that in general cases where dropout rates are below 0.5, such probabilities are minute and negligible. Thanks for pointing out pitfalls in my argument. – Buomsoo Kim Sep 11 '17 at 03:20
  • When I say how it's implemented in those libraries, I meant how they actually implemented dropout in their code. Tiny chances aside, I doubt they just left this as an uncaught error so I'm interested to know what they do in the unlikely event that all the nodes are dropped. – Dan Sep 12 '17 at 00:17