I have a scatter plot which has sample size which is equal to the number of people on x axis and median salary on y axis, I am trying to find out if the sample size has any effect on the median salary.
This is the plot:
How do I interpret this plot ?
"Find out" indicates you are exploring the data. Formal tests would be superfluous and suspect. Instead, apply standard exploratory data analysis (EDA) techniques to reveal what may be in the data.
These standard techniques include re-expression, residual analysis, robust techniques (the "three R's" of EDA) and smoothing of the data as described by John Tukey in his classic book EDA (1977). How to conduct some of these are outlined in my post at Box-Cox like transformation for independent variables? and In linear regression, when is it appropriate to use the log of an independent variable instead of the actual values?, inter alia.
The upshot is that much can be seen by changing to log-log axes (effectively re-expressing both variables), smoothing the data not too aggressively, and examining residuals of the smooth to check what it might have missed, as I will illustrate.
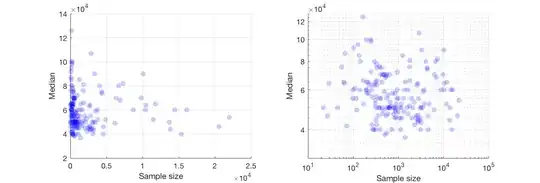
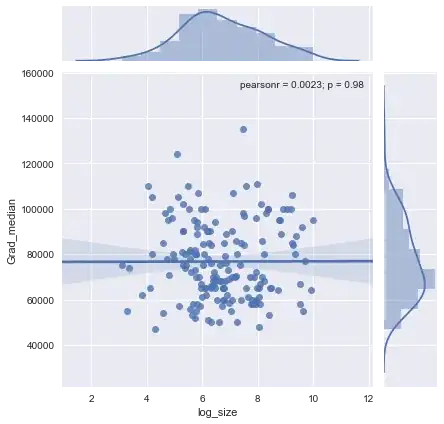
Here are the data shown with a smooth that--after examining several smooths with varying degrees of fidelity to the data--seems like a good compromise between too much and too little smoothing. It uses Loess, a well-known robust method (it is not heavily influenced by vertically outlying points).
The vertical grid is in steps of 10,000. The smooth does suggest some variation of Grad_median with sample size: it seems to drop as sample sizes approach 1000. (The ends of the smooth are not trustworthy--especially for small samples, where sampling error is expected to be relatively large--so don't read too much into them.) This impression of a real drop is supported by the (very rough) confidence bands drawn by the software around the smooth: its "wiggles" are greater than the widths of the bands.
To see what this analysis might have missed, the next figure looks at the residuals. (These are differences of natural logarithms, directly measuring vertical discrepancies between data the preceding smooth. Because they are small numbers they can be interpreted as proportional differences; e.g., $-0.2$ reflects a data value that is about $20\%$ lower than the corresponding smoothed value.)
We are interested in (a) whether there are additional patterns of variation as sample size changes and (b) whether the conditional distributions of the response--the vertical distributions of point positions--are plausibly similar across all values of sample size, or whether some aspect of them (like their spread or symmetry) might change.
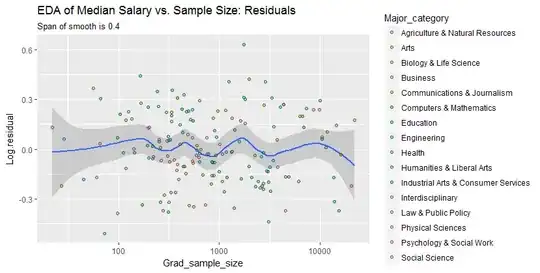
This smooth tries to follow the datapoints even more closely than before. Nevertheless it is essentially horizontal (within the scope of the confidence bands, which always cover a y-value of $0.0$), suggesting no further variation can be detected. The slight increase in the vertical spread near the middle (sample sizes of 2000 to 3000) would not be significant if formally tested, and so it surely is unremarkable in this exploratory stage. There is no clear, systematic deviation from this overall behavior apparent in any of the separate categories (distinguished, not too well, by color--I analyzed them separately in figures not shown here).
Consequently, this simple summary:
median salary is about 10,000 lower for sample sizes near 1000
adequately captures the relationships appearing in the data and seems to hold uniformly across all major categories. Whether that is significant--that is, whether it would stand up when confronted with additional data--can only be assessed by collecting those additional data.
For those who would like to check this work or take it further, here is the R code.
library(data.table)
library(ggplot2)
#
# Read the data.
#
infile <- "https://raw.githubusercontent.com/fivethirtyeight/\
data/master/college-majors/grad-students.csv"
X <- as.data.table(read.csv(infile))
#
# Compute the residuals.
#
span <- 0.6 # Larger values will smooth more aggressively
X[, Log.residual :=
residuals(loess(log(Grad_median) ~ I(log(Grad_sample_size)), X, span=span))]
#
# Plot the data on top of a smooth.
#
g <- ggplot(X, aes(Grad_sample_size, Grad_median)) +
geom_smooth(span=span) +
geom_point(aes(fill=Major_category), alpha=1/2, shape=21) +
scale_x_log10() + scale_y_log10(minor_breaks=seq(1e4, 5e5, by=1e4)) +
ggtitle("EDA of Median Salary vs. Sample Size",
paste("Span of smooth is", signif(span, 2)))
print(g)
span <- span * 2/3 # Look for a little more detail in the residuals
g.r <- ggplot(X, aes(Grad_sample_size, Log.residual)) +
geom_smooth(span=span) +
geom_point(aes(fill=Major_category), alpha=1/2, shape=21) +
scale_x_log10() +
ggtitle("EDA of Median Salary vs. Sample Size: Residuals",
paste("Span of smooth is", signif(span, 2)))
print(g.r)
Glen_b is suggesting you take the logarithm of sample_size and median salary to see if rescaling the data makes sense.
I don't know that I would agree with your belief that median salary decreases once the sample size rises above 1,000. I'd be more inclined to say there is no relationship at all. Does your theory predict that there should be a relationship?
Another way you could assess a possible relationship is to fit a regression line to the data. Alternatively, you could also use a lowess curve. Plot both lines to your data and see if anything can be teased out (I doubt there is anything overly substantive, however).
I also agree there's no relationship. I reproduced your original scatter plot (left) and made the log-log scatter plot suggested by glen_b (right).
Looks like there's no relationship to either. Correlation between log-transformed data is weak (Pearson R = -.13) and insignificant (p = .09). Depending on how much extra information you have there's maybe a reason to see some weak negative correlation, but that seems like a stretch. I'd guess that any apparent pattern you're seeing is the same effect seen here.
Edit: After looking at @famargar's plots I realized I plotted grad sample size vs non-grad median salary. I believe @sameed wanted sample size vs grad-median salary, although it's not totally clear. For the latter I reproduce @famargar's numbers, i.e. $R = 0.0022$ ($p = 0.98$) and our plots look identical.
Trying a linear regression will teach you something about this relation, as suggested in the first answer. Since It looks like you are using python plus matplotlib for this plot, you are one line of code away from the solution.
You could use seaborn jointplot, that will also display the linear regression line, the Pearson correlation coeffiecient, and its p-value:
sns.jointplot("Grad_sample_size", "Grad_median", data=df, kind="reg")
as you can see there is no correlation. Looking at this last plot, it seems log-transforming the x-variable would be useful. Let's try it:
df['log_size'] = np.log(df['Grad_sample_size'])
sns.jointplot("log_size", "Grad_median", data=df, kind="reg")
You can clearly see that - log-transformation or not - the correlation is small, and both the p-value and the confidence intervals say that it is not statistically meaningful.
This plot works as a demonstration of the central limit theorem, where the variability between samples decreases as the sample size increases. It's also the shape that you would expect with a strongly skewed variable like salary.
