1

enter image description here I measured the speeds snails fell off in a high-speed aquarium, where current was created by me opening a valve to different degrees, leading to the speeds that snails could fall-off at being set and not continuous. The snails were off two different ecotypes, and what I was examining was how the relative size of the female to the male affects her ability to hold on to the substrate below her during mating, ie, which water speeds could rip her off. I did this by gluing males onto the female's back, dividing the females into a group with males who were bigger than her glued onto her back, and males who were smaller than her glued onto her back.

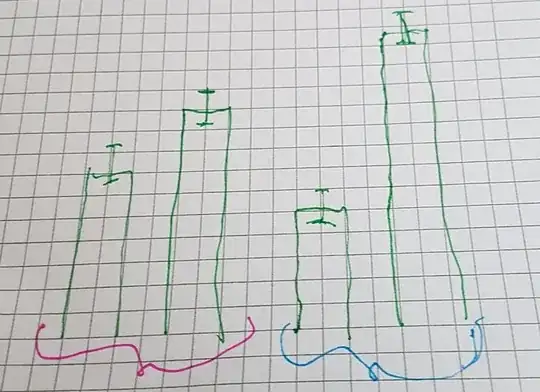
The results I got resemble what I drew in the image (the mean fall-off speed of the different relative sizes grouped according to ecotype) - when the male was bigger, the female fell off at much slower speeds compared to when the males were smaller. The ecotype to the right in the picture had lower fall-off speeds when the males were bigger compared to the ecotype to the left, and when the female was bigger it had higher fall-off speeds. These differences weren't significant, however (meaning, there was no significant difference in the mean for when the male was bigger between the "purple" and "blue" ecotype), but I would like to check if there's a significant difference between the differences between the relative sizes for each ecotype, since it seems like the difference is greater for the "blue" ecotype.

Rose Hartman
  • 2,095
  • 7
  • 30
LittleSparrow
  • 11
  • 2

2 Answers2

1

You can test this with the interaction term in a factorial ANOVA. It will test exactly what you ask for: whether the difference between the differences between the relative sizes for each ecotype is significantly different from zero. In other words, whether the effect of male size varies by ecotype.

You can run a factorial ANOVA (a 2x2 ANOVA, in this case, since you have two factors to consider and each has two levels) in pretty much any statistical software. The output will include a few different tests, but the one you're the most curious about here is the interaction term. If it's significantly different from zero, then you know that there is a difference between the differences.

Rose Hartman
  • 2,095
  • 7
  • 30
  • Does it matter if the data is continuous or not? That's why I was afraid to use ANOVA in the first place... – LittleSparrow Sep 05 '17 at 17:47
  • That depends on how many different values you have for fall-off speed. If you have more than, let's say, 5 different values, it may be reasonable to just treat that as a continuous outcome. If you prefer to respect its categorical nature, you can use a generalized linear model instead (e.g. http://www.theanalysisfactor.com/logistic-regression-models-for-multinomial-and-ordinal-variables/). Either way, you'll still enter two main effects and an interaction, and the interaction term will test the hypothesis you want. – Rose Hartman Sep 06 '17 at 16:28
0

I think this would be better suited as a comment, but I am a newcomer to Cross-Validated, and so don't have enough reputation points to comment.

That said, perhaps a multivariate t-test is what you are looking for. This is called Hotelling'S T-squared.

See these notes:

http://stat512.cwick.co.nz/lectures/24-hotellings.pdf

compbiostats
  • 1,017
  • 9
  • 18
  • 1
    Welcome to CV :) This seems fine as an answer (rather than a comment), but I think Hotelling's $T^2$ is suited to a slightly different question. It is designed to test the differences between two groups on multiple outcome variables, not the difference on one outcome variable (fall-off speed) for multiple 2-level factors. – Rose Hartman Sep 04 '17 at 21:03
  • @RoseHartman Yes, complete spur-of the moment thing on my part... clearly Hotelling's T-squared is used when one has multiple responses. Here, there is only one response - fall-off speed. So a two-factor ANOVA would probably be the most intuitive test to run quick in R or a similar program. – compbiostats Sep 04 '17 at 21:13