I am training a simple neural network in keras to fit my non-linear thermodynamic equation of state. I use backpropagation and stochastic gradient. The network approximates the equation of state but is far from being good. I added the code here:
import numpy as np
import CoolProp.CoolProp as CP
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers.core import Dense
from keras.optimizers import SGD
# vector length
nT = 20000
nP = 100
T_min = 50
T_max = 250
fluid = 'nitrogen'
# get critical pressure
p_c = CP.PropsSI(fluid,'pcrit')
p_vec = np.linspace(1,3,nP)
p_vec = (p_vec)*p_c
T_vec = np.zeros((nT))
T_vec[:] = np.linspace(T_min, T_max, nT)
rho_vec = np.zeros((nT))
print('Generate data ...')
for i in range(0,nT):
rho_vec[i] = CP.PropsSI('D','T',T_vec[i],'P',1.1*p_c,fluid)
# normalize
T_max = max(T_vec)
rho_max = max(rho_vec)
T_norm = T_vec/T_max
rho_norm = rho_vec/rho_max
print('set up ANN')
######################
model = Sequential()
model.add(Dense(200, activation='relu', input_dim=1, init='uniform'))
model.add(Dense(100, activation='relu', init='uniform'))
model.add(Dense(output_dim=1, activation='linear'))
sgd = SGD(lr=0.05, decay=1e-6, momentum=0.9, nesterov=False)
model.compile(loss='mean_squared_error', optimizer='sgd', metrics=['accuracy'])
# fit the model
history = model.fit(T_norm,rho_norm,epochs=20,batch_size=10,validation_split=0.3,shuffle=True)
predict = model.predict(T_norm,batch_size=10)
plt.plot(predict)
plt.plot(rho_norm)
plt.show()
The outcome is the following (blue is the ANN prediction):
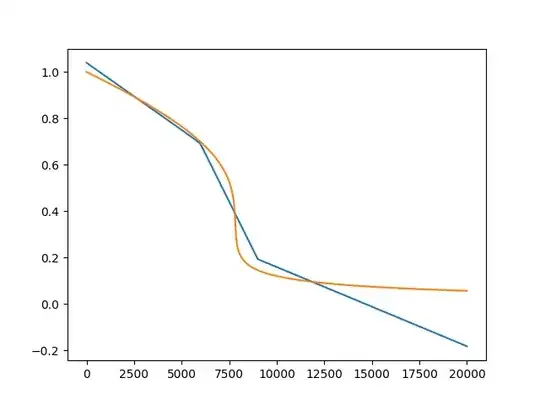
However, when I use the same model, with the same architecture on a sine it actually predicts quite well (blue again the ANN):
How can I tune my model so that it accurately predicts my thermodynamic equation of state?