My question is whether the fact that two random variables, X and Y, are symmetrically distributed implies that their ratio, Z=X/Y, is symmetrically distributed too.
-
1The relevant concept of "symmetric" for a ratio is with respect to the measure $dx/x$ rather than $dx$. See https://stats.stackexchange.com/a/29010/919 for a general definition of "symmetric" and https://stats.stackexchange.com/a/185709/919 for a detailed explanation of what symmetric with respect to $dx/x$ means. If you don't stipulate that $X$ and $Y$ are independent, then you can get *any* distribution as a ratio: given any $Z$, let $X$ and $U$ independently have the Rademacher distribution (it's symmetric), and set $Y=X/Z$ when $Z\ne 0$, $Y=U$ otherwise: $Y$ also is symmetric. – whuber Aug 23 '17 at 22:22
3 Answers
If values of $X$ and $Y$ are allowed to be negative, zero or positive, then quite a range of behaviour is possible, some perverse. Whether the variables are independent or correlated is crucial.
It is better to say what else is true, for cases you care about.
Although there are exceptions, ratios make sense mostly when both components are positive, or at least the denominator. Characteristically ratios are then (possibly highly) skewed in distribution, but their logarithms behave better. Hand waving underlines that when both values are positive, $X < Y$ implies a ratio between 0 and 1, $X = Y$ a ratio of 1 and $X > Y$ a ratio greater than 1 without definite upper limit, so in combination skewness is likely.
The easiest way to explore this is to simulate from plausible distributions for each variable, either independently (very easy) or with a stated correlation (may be trickier).
- 48,377
- 8
- 110
- 156
-
"Quite a range of behavior" includes *all possible* behaviors: see my comment to the question. (I hope it's correct!) – whuber Aug 23 '17 at 22:31
-
See George Mikes on the English and understatement at http://lib.ru/ANEKDOTY/mikes1.txt (I prefer British there, being partly Welsh.) – Nick Cox Aug 23 '17 at 22:39
-
No, not in general.
Consider X,Y both uniform on (0,1). Their ratio is not symmetric; it's heavily right skew. [However in this particular example the log of their ratio is symmetric.]
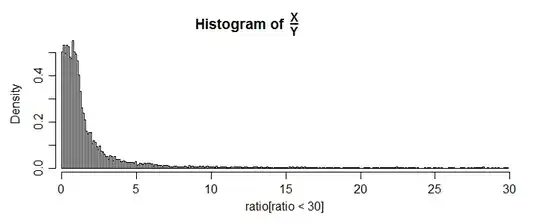
What examples did you try? Note that even if you can't do the algebra, simulation is a straightforward way to find counterexamples. Here's a histogram of the ratio of two standard uniforms:
The upper tail is much longer (the largest ratio in my sample exceeds 8000); I cut the upper tail off (about 1.6% of the sample) so you could see some detail of the shape of the main part of the distribution.
The following R code will generate a plot like that:
ratio=runif(10000)/runif(10000)
hist(ratio[ratio<30],n=300,freq=FALSE)
- 257,508
- 32
- 553
- 939
If by symmetrically distributed you mean that their distributions are symmetric around zero, then the answer is no in general, unless they are independent. For instance, take $X=Y$.
- 71
- 2
-
-
I do not see that. Unless I have misunderstood what was meant by "symmetrically distributed" (which, for me, is that $X$ and $-X$ have the same distribution). – TrivialPursuit Aug 23 '17 at 22:35
-
1That's one (narrow) notion of "symmetrically distributed." For some more general concepts, please see the links I provided in a comment to the question. In your case, $Z$ is symmetrically distributed *about its center*, which I believe is a common understanding of "symmetrical" in this context. – whuber Aug 23 '17 at 22:39
-
Spikes 1 and -1 have the same distribution in the same sense as do say uniforms with unit range centred on 0.5 and -0.5. – Nick Cox Aug 23 '17 at 22:40
-
Ok. Then, take $X$ to be a standard normal r.v., and $Y=X$ if $|X|\leq 10$, $Y=-X$ otherwise. Then, the ratio $Z=X/Y$ takes only two possible values, $-1$ and $1$, but with different probabilities. – TrivialPursuit Aug 23 '17 at 23:05