How to calculate average length of adherence to vegetarianism when we only have survey data about current vegetarians?

Question

A random population sample was surveyed. They were asked if they eat vegetarian diet. If they answered yes, they were also asked to specify how long they’ve been eating vegetarian diet without interruption. I want to use this data to calculate average length of adherence to vegetarianism. In other words, when someone becomes vegetarian, I want to know long on average they stay vegetarian. Let’s assume that:

• All respondents gave correct and accurate responses
• World is stable: popularity of vegetarianism is not changing, average length of adherence is not changing either.

My reasoning so far

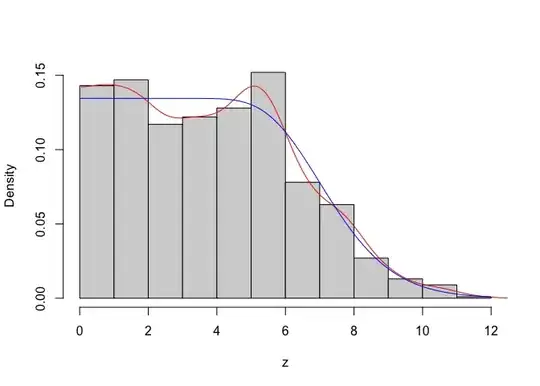
I found it helpful to analyse a toy model of the world, where at the beginning of every year two people become vegetarians. Every time, one of them stays vegetarian for 1 year and another for 3 years. Obviously, the average length of adherence in this world is (1 + 3) / 2 = 2 years. Here is a graph that illustrates the example. Each rectangle represents a period of vegetarianism:

Let’s say we take a survey in the middle of year 4 (red line). We get the following data:

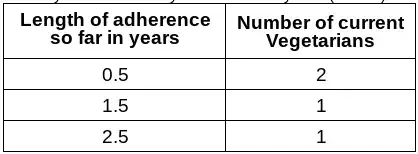
We’d get the same data if we took the survey at any year, starting year 3. If we just average the responses we get:

(2* 0.5 + 1.5 + 2.5)/4 = 1.25

We underestimate because we assume that everyone stopped being vegetarians right after survey, which is obviously incorrect. To obtain an estimate that is closer to the real average times that these participants would remain vegetarian, we can assume that on average, they reported a time about halfway through their period of vegetarianism and multiply reported durations by 2. In a large survey drawing randomly from the population (like the one I’m analysing), I think this is a realistic assumption. At least it’d give a correct expected value. However, if doubling is the only thing we do, we get average of 2.5, which is an overestimate. This is because the longer person stays vegetarian, the more likely (s)he is to be in the sample of current vegetarians.

I then thought that the probability that someone is in the the sample of current vegetarians is proportional to their length of vegetarianism. To account for this bias, I tried to divide number of current vegetarians by their predicted length of adherence:

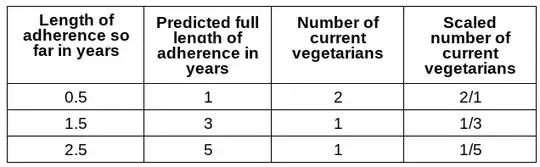
However, this gives an incorrect average as well:

(2*1 + ⅓ * 3 + ⅕ * 5)/(2 + ⅓ + ⅕) = 4 / 2.533333 = 1.579 years

It’d give the correct estimate if number of vegetarians were divided by their correct lengths of adherence:

(1 + ⅓ * (1 + 3 + 5))/(1 + ⅓ * 3) = 2 years

But it doesn't work if I use predicted lengths of adherence and they are all I have in reality. I don’t know what else to try. I read a bit about survival analysis but I’m not sure how to apply it in this case. Ideally, I would also like to be able to calculate a 90% confidence interval. Any tips would be greatly appreciated.

EDIT: It may be possible that the question above has no answer. But there was also another study that asked a random sample of people if they are/were vegetarian and how many times they've been vegetarian in the past. I also know age of everyone in both studies and some other things. Maybe this information can be used in conjunction to the survey of current vegetarians to get the mean somehow. In reality, the study I talked about is just one piece of the puzzle, but a very important one and I want to get more out of it.

Answer 1

Let $f_X(x)$ denote the pdf of adherence length $X$ of vegetarianism in the population. Our objective is to estimate $EX=\int_0^\infty x f_X(x)\;dx$.

Assuming that the probability of being included in the survey (the event $S$) is proportional to $X$, the pdf of adherence length $X$ among those included in the survey is $$ f_{X|S}(x) = \frac{xf_X(x)}{\int x f_X(x) dx}=\frac{xf_X(x)}{EX}. \tag{1} $$ At the time of being included in the survey, only a time $Z$ has passed. Conditional on $X$ and $S$, the reported time being a vegetarian is uniform with pdf $$ f_{Z|X=x,S}(z) = \frac1x, \quad \text{for } 0\le z\le x. \tag{2} $$ Elsewhere the density is zero. Hence, using the law of total probability, the overall distribution of time $Z$ passed as vegetarian among those included in the survey becomes \begin{align} f_{Z|S}(z) &= \int_0^\infty f_{Z|X=x,S}(z)f_{X|S}(x)dx \\&= \int_z^\infty \frac1x \frac{xf_X(x)}{EX}dx \\&= \frac{1-F_X(z)}{EX}, \tag{3} \end{align} where $F_X(z)$ is the cdf of $X$. Since $X$ is a positive variable $F_X(0)=P(X\le 0)=0$ and so $f_Z(0)=1/EX$.

This suggests estimating $EX$ by perhaps first estimating $f_{Z|S}(z)$ non-parametrically from the observed data $z_1,z_2,\dots,z_n$. One option is kernel density estimation, using Silverman's reflection method around $z=0$ since the domain of $f_Z(z)$ has a lower bound at $z=0$. This method applied to simulated data is shown as the red curve in the figure below. Having obtained an estimate $\hat f_Z(0)$ of $f_Z(z)$ at $z=0$, an estimate of $EX$ is then given by $\widehat{EX}=1/\hat f_Z(0)$.

This non-parametric method is not ideal however since it does not exploit the fact that $f_{Z|S}(z)$ is a non-increasing function. Also, if $f_X(0)=F_X'(0)>0$, $f_{Z|S}(0)$ may become severely underestimated and $EX$ overestimated. Finding an estimate of $EX$ in such situations without making more assumptions seems difficult, essentially because short adherence times present in this situation hardly show up in the observed data as a result of the biased sampling.

Alternatively, one could make some distributional assumptions about $f_X(x)$ and fit a parametric model by maximising the likelihood $$ L(\theta)=\prod_{i=1}^n \frac{1-F_X(z_i;\theta)}{EX(\theta)} \tag{4} $$ numerically (blue curve in above figure).

R code simulating data and implementing both methods:

# Simulate lognormal duration length in population
set.seed(1)
n <- 1e+4
x <- rlnorm(n,mean=2,sd=.2)
# Biased sampling
y <- sample(x, size=n/10, prob=x, replace=TRUE)
# Duration at time of sampling
z <- runif(length(y),min=0, max=y)
hist(z,prob=TRUE,main="")

# Compute kernel density estimate with reflection aroudn z=0
to <- max(x) + 3
fhat <- density(z,from = -to, to=to)
m <- length(fhat$y)
fhat$y <- fhat$y[(m/2+1):m] + fhat$y[(m/2):1]
fhat$x <- fhat$x[(m/2+1):m]
lines(fhat,col="red")
# Estimate of EX
1/fhat$y[1]
#> [1] 7.032448
# True value (mean of above lognormal)
exp(2+.2^2/2)
#> [1] 7.538325
# Maximum likelihood
nll <- function(theta, z) {
  - sum(plnorm(z, theta[1], theta[2], log.p=TRUE, lower.tail = FALSE)) + length(z)*(theta[1] + theta[2]^2/2)
}
fit <- optim(c(0,1),nll,z=z)
fit$par
#> [1] 1.9860464 0.2019859
EXhat <- exp(fit$par[1]+fit$par[2]^2/2) # MLE of EX
EXhat
#> [1] 7.436836
curve(plnorm(z, fit$par[1], fit$par[2], lower.tail=FALSE)/EXhat, xname="z", col="blue",add=TRUE)

Answer 2

(I've dithered over adding this, as it appears @JarleTufto has already given a nice mathematical approach; However I'm not clever enough to understand his answer, and now I'm curious if it is exactly the same approach, or if the approach I describe below ever has its uses.)

What I would do is guess an average length, and guess a few distributions around it, and then, for each, make a simulation of my population, and sample it regularly.

You said to assume the total population of vegetarians is not changing, so each time my model has someone stopping, a brand new vegetarian is created. We need to run the model for a number of simulated years to make sure it has settled down, before we can start to sample. After that I think you can take samples every simulated month (*) until you have enough to form your 90% confidence interval.

*: or whatever resolution works with your data. If people gave their answer to the nearest year, sampling every 6 months is good enough.

Out of all your guesses, you choose the mean and distribution which (averaged over all the samples you took) gives you the closest result to what your real-life survey gave.

I would iterate my guesses a few times, to narrow in on the best match.

The best distribution may not be single-peaked. The ex-vegetarians I personally can think of stopped because of major lifestyle changes (typically marrying/living with a non-vegetarian, or moving country, or falling seriously ill and a doctor suggesting it might be diet); on the other side is the power of habit: the longer you've been a vegetarian the more likely you are to carry on being one. If your data had asked age and relationship status, we could throw that in the above simulation too.