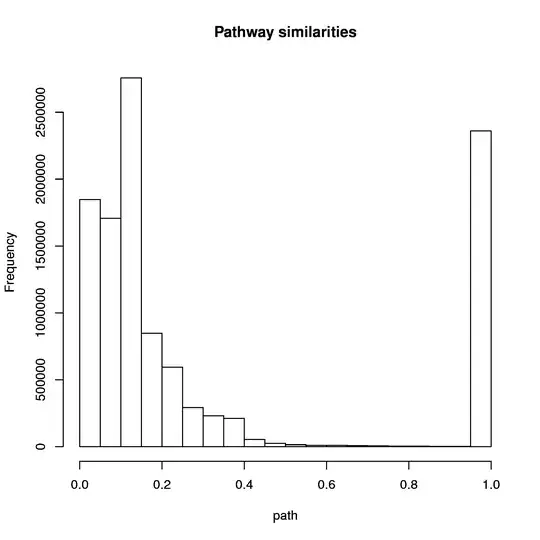
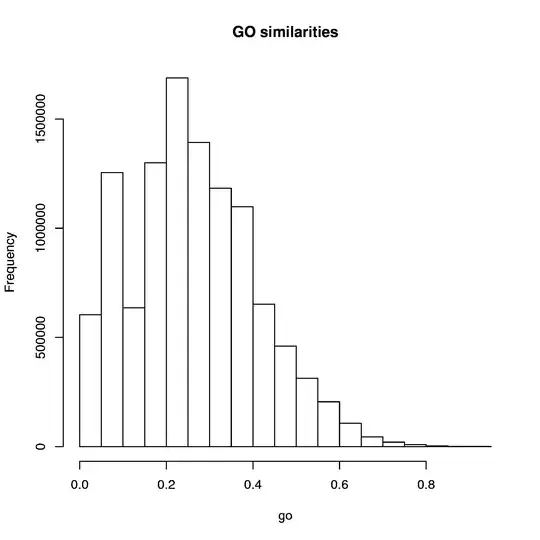
I calculate/measure two related variables $X$ and $Y$. Both of them are bounded between $[0, 1]$ (they are not probabilities though) and aren't uniformly distributed (neither randomly) as the values tend to be closer to 0.
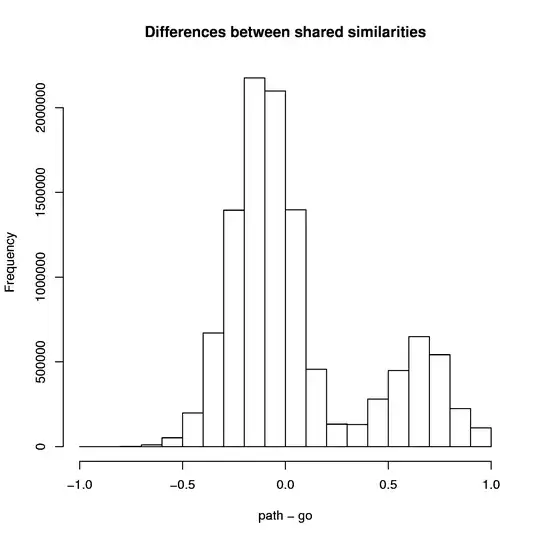
However when I subtract one variable to the other ($X-Y = Z$), $Z$ follows a normal like distribution where $\bar{z}\approx0$ and $\sigma² \approx 0.25$. It is of course bounded between $[-1, 1]$.
Surprisingly the resulting variable is centered and bell shaped. I think that there might be a reason behind it. The central limit theorem was one of the first things that came to my mind.
What can be the causes of such distribution is reached?
Note: The images are not with updated data, so they don't show as clearly the effect I describe in the question, but let's assume that.