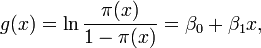Can any dataset be clustered or does there need to be some sort of pattern in the data?

Question

If a clustering algorithm (e.g., Ward's clustering algorithm; based on the way various stimuli were rated on several continuous scales) succeeds (fulfils its math. objective function) in clustering a set of data, does that suggest that there is indeed a meaningful set of clusters in the data? Or is any set of data "clusterable"? If it's the latter, how can we distinguish meaningful vs. non-meaningful clustering?

Answer 1

It seems to me there are two different primary goals one might have in clustering a dataset:

1. Identify latent groupings
2. Data reduction

Your question implies you have #1 in mind. As other answers have pointed out, determining if the clustering represents 'real' latent groups is a very difficult task. There are a large number of different metrics that have been developed (see: How to validate a cluster solution?, and the section on evaluating clusterings in Wikipedia's clustering entry). None of the methods are perfect, however. It is generally accepted that the assessment of a clustering is subjective and based on expert judgment. Furthermore, it is worth considering that there may be no 'right answer' in reality. Consider the set {whale, monkey, banana}; whales and monkeys are both mammals whereas bananas are fruits, but monkeys and bananas are colocated geographically and monkeys eat bananas. Thus, either grouping could be 'right' depending on what you want to do with the clustering you've found.

---

But let me focus on #2. There may be no actual groupings, and you may not care. A traditionally common use of clustering in computer science is data reduction. A classic example is color quantization for image compression. The linked Python documentation demonstrates compressing "96,615 unique colors to 64, while preserving the overall appearance quality":

Another classic application of clustering in computer science is to enhance the efficiency of searching a database and retrieving information.

The idea of reducing data is very counter-intuitive in a scientific context, though, because usually we want more data and richer information about what we're trying to study. But pure data reduction can occur in scientific contexts as well. Simply partitioning a homogeneous dataset (i.e., no actual clusters) can be used in several contexts. One example might be blocking for experimental design. Another might be identifying a small number of study units (e.g., patients) that are representative of the whole set in that they span the data space. In this way, you can get a subsample that could be studied in much greater detail (say, structured interviews) that wouldn't be logistically possible with the full sample. The same idea can be applied to make it possible to visualize large, complex, and high dimensional datasets. For instance, when trying to plot longitudinal data on many patients with many measurement occasions, you will typically end up with what's called a 'spaghetti plot' (due to the resulting inability to see anything of value), but it may be possible to plot a smaller number of representative patients yielding lines that can be individual discerned but that collectively represent the data reasonably well.

Other examples are possible, but the point is that a clustering can be successful without there being any actual cluster structure at all. You simply partition the space and find a smaller and more manageable dataset that can represent the total dataset by effectively spanning the space of the full data.

Answer 2

Or is any set of data "clusterable"?

Yes, all data is clusterable -- even meaningless random data.

... how can we distinguish meaningful vs. non-meaningful clustering?

Depends on what you mean by "meaningful". Sometimes the clusters are useful, often they are not. You have to decide on a case-by-case basis.

Successful clustering does not imply meaningful clusters.

Also, if the data has your kind of "meaningful" clusters, there is no guarantee that the algorithm will find those clusters.

Answer 3

Both @Ray and @Anony-Mousse have captured the ambiguity in the question by highlighting that any data set can be fed into a clustering algorithms and that this does not imply that useful clusters will be found.

To address your question from a practical point of view, you can assess the clustering tendency of a given data set to judge whether or not meaningful clusters are likely to be found.

One way to assess the clustering tendency of a data set is the Hopkins Statistic, $H$, introduced by Hopkins and Skellam, recommended by Han et al. [1] and used by Banerjee and Dave [2].

A formulation of the Hopkins Statistic is given in Wikipedia:

There are multiple formulations of the Hopkins Statistic. A typical one is as follows. Let $X$ be the set of $n$ data points in $d$ dimensional space. Consider a random sample (without replacement) of $m \ll n$ data points with members $x_i$. Also generate a set $Y$ of $m$ uniformly randomly distributed data points. Now define two distance measures, $u_i$ to be the distance of $y_i \in Y$ from its nearest neighbor in $X$ and $w_i$ to be the distance of $x_i \in X$ from its nearest neighbor in $X$. We then define the Hopkins statistic as:

$H = \frac{\sum_{i=1}^{m}u_i^d}{\sum_{i=1}^{m}u_i^d + \sum_{i=1}^{m}w_i^d}$

With this definition, uniform random data should tend to have values near to 0.5, and clustered data should tend to have values nearer to 1.

One note for interpretation is that an appropriate value for $H$ can be considered "necessary but not sufficient" to determine whether or not meaningful clusters exist. You cannot say that a non-uniform data set has meaningful clusters (i.e. a data set drawn from a single distribution) but it is true that a uniform data set does not have meaningful clusters.

[1] J. Han, J. Pei, and M. Kamber, Data mining: concepts and techniques. Elsevier, 2011. pgs 484-486

[2] Banerjee, Amit, and Rajesh N. Dave. "Validating clusters using the Hopkins statistic." In Fuzzy systems, 2004. Proceedings. 2004 IEEE international conference on, vol. 1, pp. 149-153. IEEE, 2004. DOI

Answer 4

1. Yes, any dataset can be clustered: label some points 0, some points 1 at random. Voila, it is clustered (useless, but clustered).

2. Even the "optimum" clustering of an algorithm frequently is useless. You cannot identify "usefulness" with some mathematical statistic on the input data. Instead, have a human user analyze the results.

Answer 5

No. Not every data set is truly clustered. Sometimes you're lucky to deal with homogenous data, which is by definition not clustered. On the other hand, you can almost always find clusters in the data even if they're not there, think of fortune telling on tea leaves.