2

Hello to the CrossValidated community. I could use some help.

I am struggling with the analysis of an experiment, specifically with deciding and defining in code the structure of a mixed model for analysing it.

The experimental design is as follows:

We wanted to see if there are any differences on the growth of lesions caused by different combinations of pathogens (Treatment in the data).

To investigate this we used detached leaves and inoculated them with said Treatments. Each leaf was inoculated in two spots which were averaged to give us the Area of each lesion. Measurements were done per day for all leaves in the experiment, for days 4-9 after the inoculation (Day in the data below).

Two difference cultivars of potato plants were used in the experiment (Cultivar in the data).

Leaves were arranged in boxes (Box in the data) for a complete randomized block design. Each box contained 7 leaves of each cultivar, each leaf inoculated with one of the Treatment, so a total of 14 leaves in each box.

LeafID is a unique identifier for each of leaves in the experiment.

My understanding is that Box, Cultivar, Treatment and Day are crossed factors. LeafID is crossed with Day and Box and nested within Treatment and Cultivar. I am mentioning this to check my understanding of the experimental design and furthermore to understand if it's important for defining the model. I seem to remember reading that lmer accounts for nested or crossed designs internally but can't quote a source unfortunately.

Here is a pick at my data structure in R, Day and Area are coded as double, all other variables are coded as factors

Box Cultivar Treatment  Day  LeafID Area
1   Arsenal  Control    4    121    0.0000000
1   Arsenal  Control    5    121    0.0000000
1   Arsenal  Control    6    121    0.0000000
1   Arsenal  Control    7    121    0.0000000
1   Arsenal  Control    8    121    0.0000000
1   Arsenal  Control    9    121    0.0000000
1   Arsenal  A.solani   4    21     0.1745344
1   Arsenal  A.solani   5    21     0.3062256
1   Arsenal  A.solani   6    21     0.3721086
1   Arsenal  A.solani   7    21     0.4217482
....

My understanding is that this can be analysed as either a repeated measures or a time-series design, and the choice really depends on the research question. I chose to look at this as a repeated measures design, mostly because it's easier for me to grasp the concepts and statistics involved. I am more than happy to hear differing opinions of course!

I tried to fit my model the same way Crawley does in the R Book (p,695, "Mixed-effects models with temporal pseudoreplication")

Initially we came up with the following model:

m0.full <- lme(data=DLA2, Area ~ Treatment * Cultivar * Day  ,
random = ~Day | LeafID, na.action = na.exclude ,method = "ML")

The difference from what Crawley does is that our model has extra fixed effects and their interactions Treatment * Cultivar * Day and we are using Day and its interaction as we care about the progress over time and how this affects our growth.

What I am struggling with is deciding if Cultivar should be a fixed or random effect and if including Day in the fixed effects also gives the wrong interpretation.

I've spent countless hours going through mixed model tutorials and I know that going for a very complex model is not the way to go. I guess the most confusing part is deciding what to have as fixed and random. I've seen some people suggesting you can use a factor in both fixed and random parts of the model but i have trouble grasping the concept.

I would be happy to share the entire dataset if that helps, any suggestions of the best way to do this would be welcome.

I am looking forward for some suggestions on how to handle my analysis and what could be improved.

I would be happy using either lme or lmer.

Thank you all for your time!

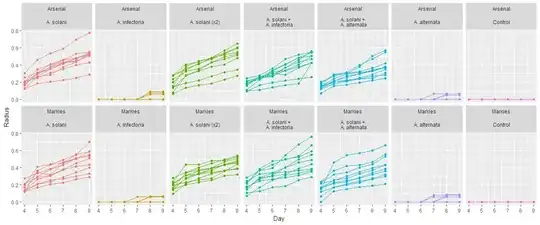
EDIT: I added a plot of my data for each different Treatment*Cultivar combination. Each panel shows the full replicates corresponding to the combination

Daily growth in lesion radius of each Treatment*Cultivar combination

UPDATE

I came up with these two models, mod.rep takes into account the repeated measures of the Day variable, while mod.time uses a time-series approach as used by Crawley(The R Book). I also accounted for heteroscedasticity using the varIdent function.

Are those models correct ?

mod.rep <- lme(data=DLA2, Radius ~ Treatment * Cultivar, random = ~ 
Day|LeafID, na.action = na.omit ,method = "ML", weights = 
varIdent(form=~1|Treatment))

mod.time <- lme(data=DLA2, Radius ~  Day * Treatment * Cultivar, random = 
~1|LeafID, na.action = na.exclude ,method = "ML", weights = 
varIdent(form=~1|Treatment))

I still have some trouble translating the random effects formulas into words...

Ioannis Baltzakis
  • 21
  • 1
  • 4
  • Does this Q&A help you https://stats.stackexchange.com/questions/4700/what-is-the-difference-between-fixed-effect-random-effect-and-mixed-effect-mode/151800#151800 – mdewey Aug 18 '17 at 12:12
  • Thank you for pointing it out. I have read it in the past and it does not help much with my particular questions regarding my dataset (like how to define the models and deal with the Day variable) – Ioannis Baltzakis Aug 18 '17 at 12:22
  • It seems to me that Cultivar, having only two levels and representing the totality of cultivars to which you might generalise, is fixed. – mdewey Aug 18 '17 at 12:35
  • If you fit a random slope model (for Day) i would have thought you also wanted to have it in your model as a fixed effect. Similarly if you have a random intercept model you usually have the intercept in the model too (which by default you will have I think). – mdewey Aug 18 '17 at 12:36
  • 1
    Thanks for the answer. Regarding the cultivar as a fixed effect, I would accept this without question if my main questions was how Cultivar affects the lesion growth together with the treatment. – Ioannis Baltzakis Aug 18 '17 at 12:44
  • 2
    In my case, I use 2 different Cultivars to get information on the effect of the Cultivar might have on the Treatment but not directly caring about it. And since the 2 cultivars are drawn from a very diverse choice of many different cultivars, let me quote Crawley : **Random effects have factor levels that are drawn from a large (potentially very large) population in which the individuals differ in many ways, but we do not know exactly how or why they differ.** – Ioannis Baltzakis Aug 18 '17 at 12:50
  • 2
    It is philosophically reasonable but not practical to treat a two-level factor as random (when using modern mixed models): see last paragraph of https://stats.stackexchange.com/questions/4700/what-is-the-difference-between-fixed-effect-random-effect-and-mixed-effect-mode/155056#155056 – Ben Bolker Aug 18 '17 at 16:16
  • That was a good read. So many people are having conflicting opinions that seems selecting something as random is a matter of preference or convenience sometimes. – Ioannis Baltzakis Aug 18 '17 at 21:01
  • So I have come up with two models, but I need some help understanding what they actually mean, one is: `lme.dla2 – Ioannis Baltzakis Oct 20 '17 at 11:14

1 Answers1

1

In section 1.5 of Pinheiro and Bates (2000) Mixed Effects Models in S and S-Plus, you can find the reference for analyzing nested factors with the nlme package, which is related to lmer. The syntax for defining the nested factors can also be found in the same passage. The book is written about S, but these functions mostly work in R without problems.

For example to introduce a free intercept for a nested factor you could write random = ~1|Box/LeafID (This is just an example, I don't say that this is relevant to the specific experiment.) You can then gradually introduce slopes in the random effects, like update(your_model, random = ~Treatment|Box/LeafID), so that to get random effects for the slope of Treatment as well, and compare model fit. (You can similarly build up your way to the triple interaction term in the fixed effects.)

nijk
  • 21
  • 3
  • So how does the use of `random=~Day|LeafID` account for the repeated measure pseudoreplication in my first model ? I don't quite get the syntax (this is what Crawley does...) – Ioannis Baltzakis Aug 29 '17 at 14:51
  • It is interpreted as a different slope ($b_{day,i}$ for each leaf. (Having in mind that Y = ... random = ~1|Box means 'assume a different mean for each Box'. https://github.com/giswqs/Learning-R/blob/master/Discovering-Statistics-Using-R/Scripts/Chapter%2013%20DSUR%20GLM4.R -- see lines 105-6 for using an lme as repeated measures. I believe it is something in the lines of `random = ~1|Box/Day` -- different intercept for each Box and each Day, because Box is the entity and Day the repeated measure. – nijk Aug 29 '17 at 15:12
  • I am not taking Box into account at all. LeafID is just the identity of each leaf. Day is where pseudoreplication occurs, unless I try and analyse as a time series. So I am assuming you mean `random = ~1|LeafID/Day` ? – Ioannis Baltzakis Aug 29 '17 at 15:14
  • If your theoretical entity is the Leaf then yes. – nijk Aug 29 '17 at 15:24
  • So is `random = ~Day|LeafID` the same as `random = ~1|LeafID/Day` ? – Ioannis Baltzakis Aug 29 '17 at 15:55
  • The first is a different (intercept and (slope for each day) for each Leaf), the latter is a different (intercept (for each day within each leaf)) plus a different (intercept for each leaf). There are $n*(m + 1)$ random effect parameters to be estimated in the former and $mn + n$ in the latter, where $n$ the number of leaves and $m$ the number of days. You can see the difference if you fit both models and then call `ranef(model1)` and `ranef(model2)` to see the difference. – nijk Aug 29 '17 at 16:22
  • Yes, indeed. Thank you, the latter does not even converge. Probably because LeafID is the smallest possible unit and just an ID really for each of the measured leaves – Ioannis Baltzakis Aug 29 '17 at 16:37
  • I would give a chance to Box in LeafID's stead though. In this case you treat Leaves as repeated measures of Boxes. That leaves you with substantially less parameters to estimate, and the information of individual leaves will be averaged in each Box's intercepts and Day slopes. I have an intuition that this approach fits with the randomized block design. Think of the original agricultural experiments by Fisher; the entities of interest were the plots receiving the treatment, not each individual plant in the plot. – nijk Aug 29 '17 at 16:52
  • So how would you write the model ? If I try to use Box instead of LeafID in mod.rep, my model does not converge. But still isn't the entity of interest the leaf here ? remember, each box has 14 leaves, 7 for each cultivar, and each one has 1 of 7 treatments applied to it – Ioannis Baltzakis Aug 29 '17 at 17:38
  • Perhaps I did not understand your block design before. Since you look for difference in growth you may want to examine the Day slope across Treatments, so perhaps compare model with `random = ~1|LeafID/Treatment` to model with `random = ~Day|LeafID/Treatment`. Significant `anova()` between the models would then mean different growth across Treatments. Perhaps also start off with `Area~1` in the formula, then start adding main effect and interaction terms one by one. – nijk Aug 29 '17 at 18:51
  • So if I want to compare Day slope (and intercept?) across treatments wouldn't the structure be `random = ~Day|Treatment` ? What does adding LeafID as you indicated achieve ? – Ioannis Baltzakis Aug 29 '17 at 20:06
  • It takes account of the fact that the measures come from the same individuals over time. If you didn't want that I think you could just look at the interaction term Cultivar * Treatment. – nijk Aug 29 '17 at 20:44
  • I do care for taking into account that measurements come from the same individuals. As you suggested I tried `random = ~Day|LeafID/Treatment` and `random = ~1|LeafID/Treatment`. With the first option the model does not converge. I would have to do it like this `mod.timeAR – Ioannis Baltzakis Aug 29 '17 at 20:48