Here is a counter example using randomly generated data and R:
library(MASS)
library(leaps)
v <- matrix(0.9,11,11)
diag(v) <- 1
set.seed(15)
mydat <- mvrnorm(100, rep(0,11), v)
mydf <- as.data.frame( mydat )
fit1 <- lm( V1 ~ 1, data=mydf )
fit2 <- lm( V1 ~ ., data=mydf )
fit <- step( fit1, formula(fit2), direction='forward' )
summary(fit)$r.squared
all <- leaps(mydat[,-1], mydat[,1], method='r2')
max(all$r2[ all$size==length(coef(fit)) ])
plot( all$size, all$r2 )
points( length(coef(fit)), summary(fit)$r.squared, col='red' )
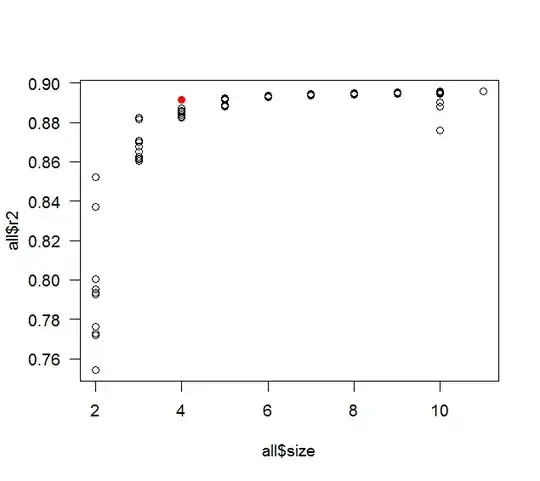
whuber wanted the thought process: it is mostly a contrast between curiosity and laziness. The original post talked about having 10 predictor variables, so that is what I used. The 0.9 correlation was a nice round number with a fairly high correlation, but not too high (if it is too high then stepwise would most likely only pick up 1 or 2 predictors), I figured the best chance of finding a counter example would include a fair amount of collinearity. A more realistic example would have had various different correlations (but still a fair amount of collinearity) and a defined relationship between the predictors (or a subset of them) and the response variable. The sample size of 100 was also the 1st I tried as a nice round number (and the rule of thumb says you should have at least 10 observations per predictor). I tried the code above with seeds 1 and 2, then wrapped the whole thing in a loop and had it try different seeds sequentially. Actually it stopped at seed 3, but the difference in $R^2$ was in the 15th decimal point, so I figured that was more likely round-off error and restarted it with the comparison first rounding to 5 digits. I was pleasantly surprised that it found a difference as soon as 15. If it had not found a counter example in a reasonable amount of time I would have started tweaking things (the correlation, the sample size, etc.).
