Since I'm relatively new to regularized regressions, I'm concerned with the hughe differences lasso, ridge and elastic nets deliver.
My data set has the following characteristics:
- panel data set: > 900.000 obs. and over 50 variables
- highly unbalances
- 2-5 variables are highly correlated.
To select only a subset of the variables I used penalized logistic regression fitting the model: $\frac{1}{N} \sum_{i=1}^{N}L(\beta,X,y)-\lambda[(1-\alpha)||\beta||^2_2/2+\alpha||\beta||_1] $
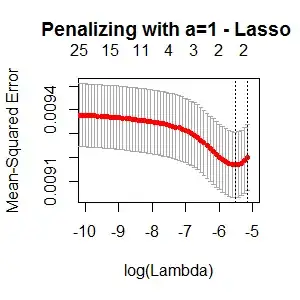
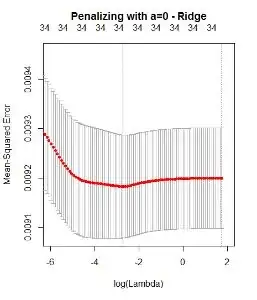
To determine the optimal $\lambda$ I used cross validation which yileds the following results:
The elastic net looks quite similar to the Lasso, also proposing only 2 Variables.
So my main question is: why do these approaches deliver so different results? According to the Lasso, I only do have 2 variables in the final model and according to the Ridge, I do have 34 variables?
So in the end - which approach is the right one? And why are the results so extremely different?
Thanks a lot!