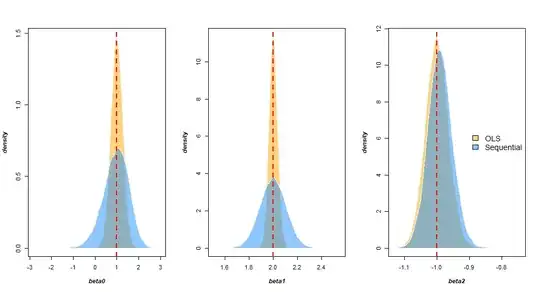
I'd like help considering two different strategies in performing my regression.
Strategy 1:
model the output y as a linear combination of input variables x1 through x3:
fit = lm(y ~ x1 + x2 + x3)
Strategy 2:
model the output y with a linear relationship single input variable x1, and then model the residual of that through x2 etc:
firstFit = lm(y ~ x1)
firstResidual = y - predict(firstFit)
secondFit <- lm(firstResidual ~ x2 + 0) # Only one intercept
secondResidual = firstResidual - predict(secondFit)
thirdFit <- lm(secondResidual ~ x3 + 0) # Only one intercept
Questions:
- What are the differences between these two strategies?
- Can I expect that the "quality" of the coefficients in Strategy 1 to be uniform across
X, and in Strategy 2 to not be? - Strategy 1 seems generally the way to go, what would be a circumstance where Strategy 2 would be better?
- If I believe that the "truth" is that
yis the output of a nested set of functions:y = f1(x1, f2(x2, f3(x3))),
would Strategy 2 be an appropriate way to model the system?