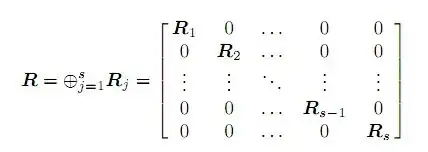I have a time series linear regression with a really high R-Squared. I'm a little bit apprehensive to start using it though because of the residual plot. I know that the residuals are supposed to be random and have a mean of 0.
Here is a plot of my residuals:
The mean is approximately 0, but as you can see, the residuals do not look like the nice little cloud that are always in the linear regression examples. The residuals are particularly low around 20650 and particularly high a little above 20700 with a little bit of a parabola look between 20500 and 20700.
I'm wondering if I should not be content with my model until the residuals look like the perfect cloud of random points or if that is overly idealistic. Are there any statistical procedures to measure whether or not the residual assumptions are met?