4

For practical reasons I need to eliminate some columns of a matrix based on how close they are to being a linear combination of other columns (Not looking for a regularizing method like LASSO or anything here -- the constraints are related to hardware capabilities). I feel like this should be a standard test of some kind as opposed to a custom for-loop over the columns in which I fit a linear model of the other variables to get an L2 distance (or similar metric) to sort by. Ideally it could be done in an iterative fashion down to a certain number of columns (features) that I preset. Is there some standard method for this?

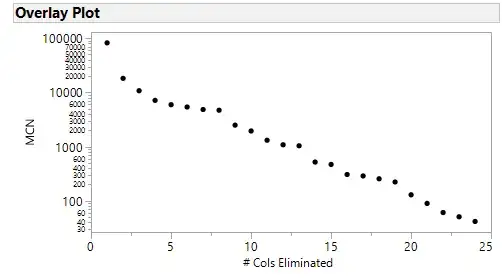
Note #1: I did try iterative elimination of columns based on the column which caused the largest decrease in matrix condition number as recommended by some (I standardized all the columns first). I found the pattern very interesting in that it wasn't a smooth curve (after logrithmic transformation) but had "intervals" if you will of decaying change with a sort of discontinuous jump between them. Is this expected behavior?

MCNiteration

Note #2: I also took another look at PCA in terms of the Eigenvectors associated with the smallest eigenvalue, but the process of sequential elimination wasn't as obvious as the matrix condition number.

JPJ
  • 1,161
  • 8
  • 15
  • 1
    reduced row echelon form or PCA? https://stats.stackexchange.com/questions/16327/testing-for-linear-dependence-among-the-columns-of-a-matrix – hamster on wheels Aug 04 '17 at 20:32
  • hmm don't think so -- those are for determination of linear dependence and/or dimensional reduction but offer no insight into a quantification/degree of "closeness" by which one feature/column can be approximated by the rest of the features/columns. – JPJ Aug 04 '17 at 21:17
  • 3
    PCA's eigenvalue tells the cost for dropping the eigenvector in reconstructing the original matrix from the eigenvalue and eigenvector. So that tells the "degree" of linear dependence. The question is if doing a full diagonalization of your data is too costly. Actually you can try to find just the few smallest eigenvalues and corresponding eigenvectors for your matrix. that should be better for the computer. Probably there are still some details to fix. – hamster on wheels Aug 04 '17 at 21:32
  • @rxu I'm interested in your answer but would like to see you expand on it in a way that explains how the eigenvalue "cost" is related to the "closeness" (or degree as you call it) by which a given feature is to being approximated by a linear combination of the others. I've seen so many interpretations of eigenvalues and eigenvectors but this is yet a slightly different viewpoint I think. – JPJ Aug 05 '17 at 14:48
  • 4
    I believe the question should be reopen, it is enough statistical. – ttnphns Aug 05 '17 at 14:50
  • python3 program: import numpy as np;N = 4;M = 2;thres = 0.000001;x = np.random.normal(0,1,N*N).reshape(N,N);x[:,:M]= 1/N;x /= np.sum(x, axis=0);print("matrix\n", x);evalue, evec = np.linalg.eig(x);evalue = np.abs(evalue);evec = np.abs(evec);evalue[evalue < thres] = 0;evec[evec < thres] = 0;print("evec for nearly zero evalue");k=[print(evalue[i], evec[:, i]) for i in range(N) if evalue[i] == 0] – hamster on wheels Aug 05 '17 at 16:09
  • 1
    The answer about PCA in that link says if eigenvalues are close to zero, the corresponding eigenvectors have non-zero entries correspond to the columns that are nearly linearly dependent to each other. Usually PCA just keep eigenvectors for large eigenvalues. In your case, you should find eigenvectors for eigenvalues that are closest to zero. – hamster on wheels Aug 05 '17 at 16:17
  • I don't see this as off topic due to its computational focus, but it does seem to be *too broad* to me at present. If that were addressed, it could be reopened, IMO. – gung - Reinstate Monica Aug 05 '17 at 18:29
  • @gung understood -- but part of the issue is that there isn't a solid set of methods to "rank" features in terms of their redundancy from what I'm seeing (i.e. in terms of the unique information they hold). Thus turning into a discussion forum a bit as I try things out and more folks post ideas, but I'm having trouble refining the question. – JPJ Aug 05 '17 at 20:42
  • That's a legitimate problem (in some ways I think the SE system should be looser), but it is still against SE policy. I don't have a good solution here, or any great suggestions for improvement, I'm afraid. – gung - Reinstate Monica Aug 05 '17 at 21:07
  • If you have an issue with consistency of closure, please raise it on meta, not in your question. Could you edit your question to remove the complaint, but keep any information you added that would be relevant to your question. – Glen_b Aug 06 '17 at 10:15
  • I think this question might be a duplicate of https://stats.stackexchange.com/questions/16327/. Although that one explicitly asks only to detect collinearity, my answer there extends this to the question of detecting *approximate* collinearity and shows how the SVD provides a natural (and optimal) way to do so. I have also answered this question, although posed in a different way, at https://stats.stackexchange.com/questions/245972. Finally, my answer at https://stats.stackexchange.com/a/173701/919 discusses the connections between the SVD, VIF, and condition numbers. – whuber Aug 16 '17 at 16:14

1 Answers1

1

One way I can think of is using matrix condition number. According to Wikipedia:

In the field of numerical analysis, the condition number of a function with respect to an argument measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input.

...

In linear regression the condition number can be used as a diagnostic for multicollinearity.[1][2]

[1] Belsley, David A.; Kuh, Edwin; Welsch, Roy E. (1980). "The Condition Number". Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New York: John Wiley & Sons. pp. 100–104. ISBN 0-471-05856-4.

[2] Pesaran, M. Hashem (2015). "The Multicollinearity Problem". Time Series and Panel Data Econometrics. New York: Oxford University Press. pp. 67–72 [p. 70]. ISBN 978-0-19-875998-0.

Here is a toy example:

> set.seed(0)
> x=runif(100)
> A1=cbind(x,x+runif(100)*1e-8)
> A2=cbind(x,2*x)
> kappa(A1)
[1] 329716417
> kappa(A2)
[1] 5.742016e+15
Haitao Du
  • 32,885
  • 17
  • 118
  • 213
  • 1
    Could you elaborate on your answer to help the OP use this approach to remove specific columns selectively? – EdM Aug 04 '17 at 18:02
  • I didn't know about this, but seems to have potential. As mentioned by Edm I would also like the answer expanded more though if possible. – JPJ Aug 04 '17 at 18:12
  • So after searching around a bit it is still unclear to me if it is a good idea to standardize columns prior to calculating the matrix condition number. It seems I would want to since this is based on a Norm calculation, but a confirmation would be nice. – JPJ Aug 04 '17 at 21:15
  • Although a large condition number *detects* collinearity, it does not *find* the basis of it as requested here. – whuber Aug 16 '17 at 16:15