We can think of any supervised learning task, be it regression or classification, as attempting to learn an underlying signal from noisy data. Consider the follwoing simple example:
Our goal is to estimate the true signal $f(x)$ based on a set of observed pairs $\{x_i, y_i\}$ where the $y_i = f(x_i) + \epsilon_i$ and $\epsilon_i$ is some random noise with mean 0. To this end, we fit a model $\hat{f}(x)$ using our favorite machine-learning algorithm.
When we say that the OLS estimator is unbiased, what we really mean is that if the true form of the model is $f(x) = \beta_0 + \beta_1 x$, then the OLS estimates $\hat{\beta}_0$ and $\hat{\beta}_1$ have the lovely properties that $E(\hat{\beta}_0) = \beta_0$ and $E(\hat{\beta}_1) = \beta_1$.
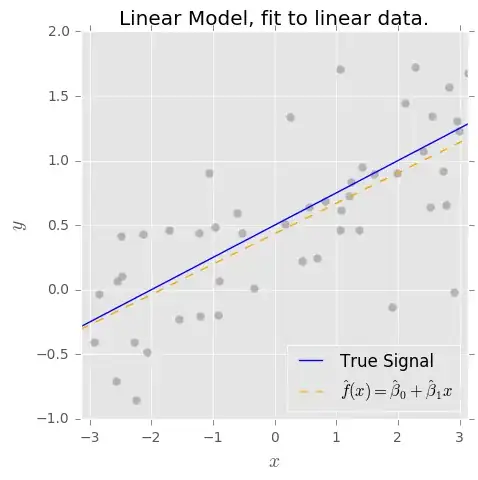
This is true for our simple example, but it is very strong assumption! In general, and to the extent that no model is really correct, we can't make such assumptions about $f(x)$. So a model of the form $\hat{f}(x) = \hat{\beta}_0 + \hat{\beta}_1 x$ will be biased.
What if our data look like this instead? (spoiler alert: $f(x) = sin(x)$)
Now, if we fit the naive model $\hat{f}(x) = \hat{\beta}_0 + \hat{\beta}_1 x$, it is woefully inadequate at estimating $f(x)$ (high bias). But on the other hand, it is relatively insensitive to noise (low variance).
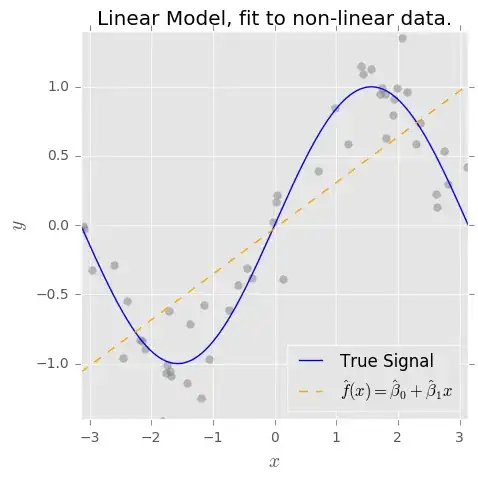
If we add more terms to the model, say $\hat{f}(x) = \hat{\beta}_0 + \hat{\beta}_1x + \hat{\beta}_2x^2 + ... \hat{\beta}_p x^p$, we can capture more of the "unkown" signal by virtue of the added complexity in our model's structure. We lower the bias on the observed data, but the added complexity necessarily increases the variance. (Note, if $f(x)$ is truly periodic, polynomial expansion is a poor choice!)
But again, unless we know that the true $f(x) = \beta_0 + \beta_1 sin(x)$, our model will never be unbiased, even if we use OLS to fit the parameters.




