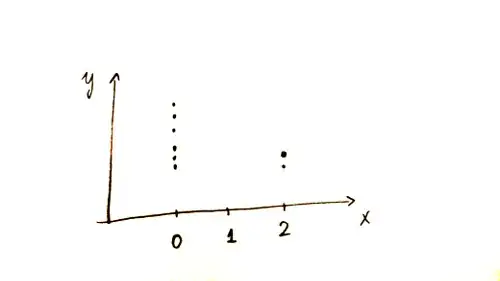
I am trying to fit a function $f$ to the data pictured below:
For $\hat{f}(0)$ I can take the sample mean of the 6 observations at $0$, for $\hat{f}(2)$, I average the 2 at 2.
For $\hat{f}(1)$, I don't have any observations. OLS will give me
$$\hat{f}(1) = \frac{\hat{f}(0) + \hat{f}(2)}{2}$$
Instead, I'd like a weighted average, where $\hat{f}(0)$ is given more weight, because I trust it more.
How can this idea be formulated in terms of a probabilistic model/loss function? I'm sure this problem has been studied extensively.