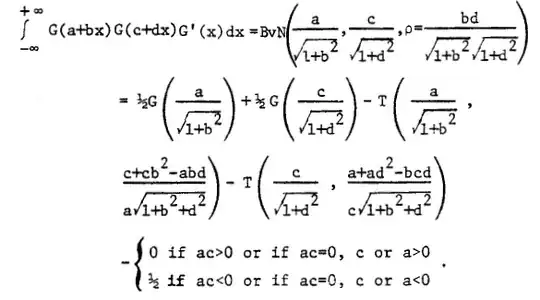Calculating the integral of two normal CDFs with a normal distribution

Question

I'm trying to calculate: $$\int\Phi((x-\mu_{1})/\sigma_{1})*\Phi((x-\mu_{2})/\sigma_{2})*\phi(x)dx$$ where $\Phi$ and $\phi$ are the standard normal cumulative distribution function and probability density function, respectively.

The reason I'm trying to do this is that I want to use truncated variational posteriors in a variational inference model and I need to find out the normalizing constant for the combination of a normal with a differential approximation of a step function.

There is some stuff calculating $E[\Phi((x-b)/a)]$ here on Math Overflow. However, I need two truncation terms and not just one. I can't think how to extend the proof given in the link to two normal CDFs. I've tried writing $N(\mu,\sigma)$ as $\mu + \sigma*N(0,1)$ for the CDFs and doing u substitution but that seems to not work (I get infinities usually). Any help would be appreciated. Thanks!

Do you really mean $\Phi((x - \mu_1) / \sigma_1) \Phi((x - \mu_1) / \sigma_1)$, or should it be $\Phi((x - \mu_1) / \sigma_1) \Phi((x - \mu_2) / \sigma_2)$? — Danica, Jul 24 '17 at 20:02
Assuming you meant exactly what you wrote, you might find the techniques at https://stats.stackexchange.com/questions/61080 useful. Otherwise, if @Dougal's suspicion is correct, you will need to integrate numerically. — whuber, Jul 24 '17 at 20:21

score 5 · Answer 1 · answered Jul 25 '17 at 09:46

This integral: $$ \int_\mathbf{R} \Phi\left(\frac{x-\mu_1}{\sigma_1}\right)\Phi\left(\frac{x-\mu_2}{\sigma_2}\right) \phi(x) \, \mathrm dx $$ can be expressed like this:

where $T$ is the Owen $T$-function and $\textrm{BvN}$ is the bivariate normal distribution function.

Source: Owen, A table of normal integrals, 1980.

Check:

> integrand <- function(x, a, b, c, d){
+   pnorm(a+b*x)*pnorm(c+d*x)*dnorm(x)
+ }
> a <- 1; b <- 2; c <- 3; d <- 4
> integrate(integrand, lower=-Inf, upper=Inf, a=a, b=b, c=c, d=d)
0.6404609 with absolute error < 4.7e-05
> 
> rho <- b*d/(sqrt(1+b^2)*sqrt(1+d^2))
> Sigma <- matrix(c(1,rho,rho,1), ncol=2)
> mvtnorm::pmvnorm(upper=c(a/sqrt(1+b^2), c/sqrt(1+d^2)), sigma = Sigma)
[1] 0.6404609
attr(,"error")
[1] 1e-15
attr(,"msg")
[1] "Normal Completion"
> 
> library(OwenQ)
> pnorm(a/sqrt(1+b^2))/2 + pnorm(c/sqrt(1+d^2))/2 -
+   OwenT(a/sqrt(1+b^2), (c+c*b^2-a*b*d)/a/sqrt(1+b^2+d^2)) -
+   OwenT(c/sqrt(1+d^2), (a+a*d^2-b*c*d)/c/sqrt(1+b^2+d^2))
[1] 0.6404609

score 1 · Answer 2 · edited Jul 25 '17 at 09:50

The value of the integral can be interpreted as the probability that a standard normal random variable $X$ is larger than $\max(Y,Z)$ where $Y$ and $Z$ are independent $N(\mu_1,\sigma_1^2)$ and $N(\mu_2,\sigma_2^2)$ random variables. Note that $$P\{Y < X, Z < X\mid X = x\} = \Phi\left(\frac{x-\mu_1}{\sigma_1}\right)\Phi\left(\frac{x-\mu_2}{\sigma_2}\right)$$ by independence and the law of total probability then tells us that \begin{align} P\{X > \max(Y,Z)\} &= \int_\mathbf{R}P\{Y < X, Z < X\mid X = x\} \phi(x) \, \mathrm dx\\ &= \int_\mathbf{R} \Phi\left(\frac{x-\mu_1}{\sigma_1}\right)\Phi\left(\frac{x-\mu_2}{\sigma_2}\right) \phi(x) \, \mathrm dx \end{align} which, as whuber's comment points out, has no known analytical solution in simple terms. Numerical integration is necessary except in some special cases (e.g. the answers to this recent question or this earlier one).

Calculating the integral of two normal CDFs with a normal distribution

2 Answers2