General question regarding Over-fitting vs Complexity of Models

Question

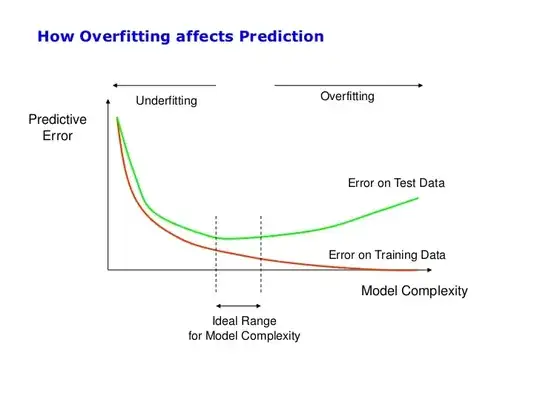
Increasing complexity of models results in over-fitting of the training data, is the inverse true too? Assuming that my chosen classifier is able to fully fit the training set (i.e 100% accuracy), should I then search for the parameters that produces the least complex model but yet retaining 100% accuracy for the training set? Will this generally be the best generalization for an unseen test set? Or it depends? Or we can't tell and we should use CV to find the best parameters? This dilemma often happens when I try to choose the best number of hidden nodes for my neural nets.

However, usually for my test set, my test error is shifted much further to the right as seen in the graph below. Point A is the ideal complexity. Point B is the least complexity where the train set does not underfit. From the first graph, point B is right of point A, whereas from my experiments I often get point A right of point B. Just wondering is there any explanation why?

Answer 1

First of all, something obvious: if you have a figure of merit that stays constant over a relevant range of your search space (e.g. complexity parameter) then that figure of merit is not suitable as target functional for optimization. The exception are, of course, models that are truly equivalent for the application at hand. The problem here is, that all those indistinguishable models are not equivalent in their predictive ability.

You may consider switching the figure of merit you optimize:

• instead of accuracy, use a (strictly) proper scoring rule (e.g. Brier's score or log loss). These work on metric score predictions (i.e. one step before applying the threshold/cutoff that generates class labels) and have their optimum for a classifier that correctly images the posterior probability of the test cases. This is what you need for successful optimization. In addition, they react more sensitively to slight deviations from optimal prediction and thus avoid the problem of choosing between seemingly equivalent models that are in fact not equal.

• A discrepancy between training and test error as in your example graphs means that the training error is far too optimistic to tell you anything useful for the model complexities you actually consider for the final model. You need to switch to a better scheme for generating test cases for the optimization, e.g. another level of nesting in your resampling validation (out-of-bootstrap or cross validation).

• A third point that you should keep in mind is: you only show point estimates for accuracy, but not the corresponding random uncertainty (variance). Variance increases with model complexity as models become unstable. Aggressive optimization in such a situation can lead to overfitting even with resampling validated or hold-out-type figures of merit: you pick a hyperparameter that accidentally works well with this split or this test set. A symptom of this is that the inner test figure of merit used by the optimization looks better than the final validation on a completely independent outer test set.
  In this situation, you should restrict your model complexity to be less than the apparent optimum. E.g. the Elements of Statistical Learning (Ch. 7.10.1 K-Fold Cross Validation) suggest the heuristic "complexity where figure of merit falls below optimum + 1 standard error".