In an earlier question, I asked about the limiting distribution of the square root of the absolute value of the sum of $n$ i.i.d. random variables each with finite non-zero mean $\mu$ and variance $\sigma^2$. The answer was (after a suitable location and scale adjustment) a standard normal distribution.
This time I am asking about the case where $\mu=0$. I know and can demonstrate the answer, but I am interested in whether the resulting distribution has any other uses.
So suppose $X_1, X_2, \ldots, X_n$ are i.i.d. random variables with zero mean and positive variance $\sigma^2$. If $\displaystyle Z=\sqrt{\left|\sum_{i=1}^n X_i\right|}$ then $\displaystyle \dfrac{Z}{\sqrt[4]{n} \, \sqrt{\sigma}} \ \xrightarrow{d}\ W$ as $n$ increases, where $W$ has the distribution of the square root of a standard half-normal random variable.
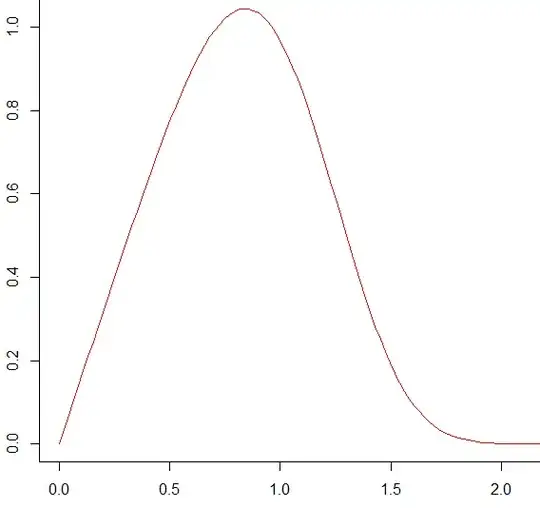
- The density of $W$ is $f(x)=\sqrt{\dfrac{8}{\pi}}\,x\,e^{-x^4/2}$ for $x \ge 0$
- The mean of $W$ is $\dfrac{\sqrt[4]{2}\;\Gamma\left(\frac34\right)}{\sqrt{\pi}} \approx 0.822179$
- The variance of $W$ is $\sqrt{\dfrac2\pi}{\left(1- \dfrac{\Gamma\left(\frac34\right)^2}{\sqrt{\pi}}\right)} \approx 0.1219063$
- The standard deviation of $W$ is then about $0.3491509$
- So the mean and standard deviation of $Z$ could be approximated by those of $W$ scaled up by a factor of $\sqrt[4]{n} \, \sqrt{\sigma}$
The density of $W$ looks like the following chart. It has a very light tail, with $\mathbb{P}(W>2) < 0.00007$
Has anybody come across this distribution before?