My case is quite simple.
Customers are faced with series of choices of unique alternatives. For example:
- Customer 1 chooses one of 1,2,3,4,5,6
- Customer 1 chooses one of 7,8,9
- Customer 2 chooses one of 10,11,12,13
- Customer 2 chooses one of 14,15,16 etc
All the alternatives 1,2,... are unique and can't be naturally categorized. Every alternative has the same set of attributes. I'm interested in effects of alternatives' attributes on customer's choice.
For example, a person travels through a country and chooses a hotel to stay. Every day she is in a new city and the hotels to choose are completely new. The hotels differ by price and rating. One can expect that price has negative and rating has positive effect on customer's choice.
It seems that multinomial logit is not applicable here as it needs a categorical dependent variable.
My understanding is that there should be a simple statistical method for the problem because mathematics behind it seems to be quite clear. Indeed, assume the alternatives have 2 continuous attributes.
Let $U= \alpha X+\beta Y$ be the utility function of the attributes $X$ and $Y$. Every observation can be represented by several points on the $(X,Y)$-plane. Assume there are four alternatives $A, B, C, D$ and $A$ is chosen. For every vector with tail at $A$ calculate the fraction of points in the left half-plane given by this vecor. Thus one gets a circle partitioned into the union of arcs and corresponding numbers so that the sum of two numbers corresponding to the opposite arcs equals 1.
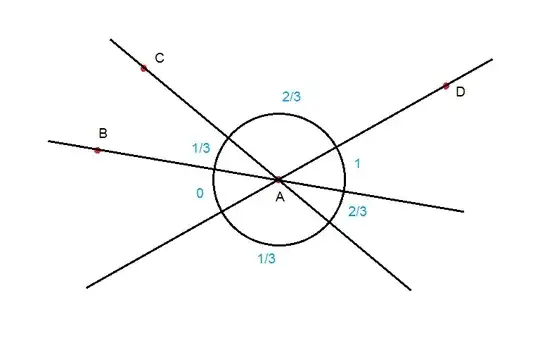 After aggregation a similar partitioned circle appears. Then the tangents of the vectors from the arc with maximal number are the estimators of $\alpha/\beta$.
After aggregation a similar partitioned circle appears. Then the tangents of the vectors from the arc with maximal number are the estimators of $\alpha/\beta$.