0

for example the data has a binary response y, a numerical predictor week, and some categorical/factor predictors: ap, hilo, ID, trt:

   y ap hilo week  ID     trt
1  y  p   hi    0 X01 placebo
2  y  p   hi    2 X01 placebo
3  y  p   hi    4 X01 placebo
4  y  p   hi   11 X01 placebo
5  y  a   hi    0 X02   drug+
6  y  a   hi    2 X02   drug+
7  n  a   hi    6 X02   drug+
8  y  a   hi   11 X02   drug+
9  y  a   lo    0 X03    drug
10 y  a   lo    2 X03    drug

Logistic regression result looks like:

Coefficients: (4 not defined because of singularities)
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.550e+00  1.251e+00   2.038 0.041561 *  
app          1.924e+01  8.359e+03   0.002 0.998164    
hilolo      -1.562e+00  1.617e+00  -0.966 0.334074    
week        -2.127e-01  6.377e-02  -3.335 0.000852 ***
IDX02       -2.525e-01  1.721e+00  -0.147 0.883337    
IDX03        2.081e+01  7.562e+03   0.003 0.997804    
IDX04        1.572e+00  1.127e+04   0.000 0.999889    
IDX05        1.572e+00  1.127e+04   0.000 0.999889    
...

Null deviance: 217.38  on 219  degrees of freedom
Residual deviance: 118.51  on 169  degrees of freedom
AIC: 220.51

Number of Fisher Scoring iterations: 19 It tells us for predictor ID, the baseline is ID == 'X01' (not shown in result). Comparing ID == 'X02' to '01', the change is not significant, because the p-value is 0.883337.

My question is how do you compare ID == 'X02' to 'X03'? The log adds changes by 2.081e+01 - (-2.525e-01), what error do I compare this difference to, and how to calculate p value?

Can somebody give an example using ID == 'X02' to 'X03' please? Thank you.

I leave the code later because my question is only about theory. Code in R:

library(MASS)
library(stats)

data('bacteria')
dat = bacteria

glm_model = glm(y ~ ., family = binomial, data = dat)
summary(glm_model)

What I know (not very sure, and would like to get verified)

each coefficient has it's estimate and std.error, because there's a population of many different values of this coefficient calculated by using differently sampled data.

So comparing ID == 'X02' to 'X03' is to compare the mean of two populations. I read this post, so 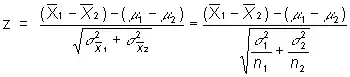enter image description here

so, is delta(x1bar) in the equation the std.error in the glm result? I don't need to divide by n any more, right (since the std.error in the glm result in already the standard deviation of the mean)?

Comparing ID == 'X02' to 'X03':

z = (-2.525e-01 - 2.081e+01) / sqrt(1.721e+00^2 + 7.562e+03^2)
= -0.002785

is this correct? Thanks-

XYZ
  • 163
  • 6
  • If you are looking for the coefficients and hypothesis tests to reflect differences between adjacent levels (e.g. `X01` vs `X02`, `X02` vs `X03`, `X03` vs `X04`, etc.), use forward-difference coding. See https://stat.ethz.ch/R-manual/R-devel/library/MASS/html/contr.sdif.html and https://stats.idre.ucla.edu/r/library/r-library-contrast-coding-systems-for-categorical-variables/ . – MAB Jul 06 '17 at 01:26
  • thank you @MAB! I think I prefer not to present in a difference coding - because in practice I have many categorical predictor, for some of them I want to compare adjacent levels, whereas for others I compare all levels to the baseline. If I use the difference coding for some the predictors, it may look confusing - what do you think? Thank you- – XYZ Jul 06 '17 at 03:00
  • In that case I suggest you look into the `multcomp` package. – MAB Jul 06 '17 at 04:44
  • This Q&A although not a direct answer to your question might be useful as I think your answer will also involve the covariance matrix of your coefficients https://stats.stackexchange.com/questions/93303/variance-covariance-matrix-interpretation – mdewey Jul 07 '17 at 06:14

0 Answers0