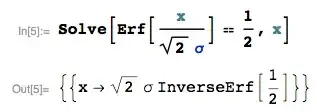Expectation of Median of Absolute Random Variables

Question

Let $X_1, X_2,..., X_n$ from $N(0,\sigma^2)$.

What I want to get is not $E(median(|X|))$ , but $E(median(|X_1|,|X_2|,...,|X_n|))$

---

Reason why I need it is because I'm studying LOWESS, and in using bisquare wieght function, weight of residuals within the 6m(m is a median) will be 1, elsewhere its weight would be 0. And the reason why we took 6m is because, m=$\frac{2}{3}\sigma$, 6m=4$\sigma$. As $P(|Z|\ge4\sigma)$ is almost zero, weights are corresponding.

So I need a conclusion that $E(median(|X|))=\frac{2}{3}\sigma$, which I can't derive.

=============Edit================

There is a huge error in denoting $E(median(|X|))$. As I meant it by the expectation of the median of $|X_1|,|X_2|,...,|X_n|$, It should have been $E(median(|X_1|,|X_2|,...,|X_n|))$. Sorry for the confusion.

And I will also edit the title from 'Expectation of Absolute median' to 'Expectation of Median of Absolute Random Variables' (Please recommend other titles) as soon as we have the conclusion. Thank you so much for the interest.

Answer 1

The OP's question is somewhat confused. But, I think I have been able to figure out what he is asking. We are given a parent random variable $Z \sim N(0,\sigma^2)$. The pdf of $X =|Z|$ is a half-Normal with pdf say $f(x)$:

which appears thus, as parameter $\sigma$ changes:

The cdf $P(X<x)$ is:

where I am using the mathStatica Prob function to automate.

The population median is the value of $x$ such that $P(X<x) = \frac12$, which yields:

The OP asks to show that something is the same as $\frac23 \sigma$. The median is NOT equal to $\frac23 \sigma$, but $\frac23 \sigma$ is a rather good simple approximation of the correct solution which we have just derived. To see this, the following diagram compares:

• the EXACT median, plotted as a function of $\sigma$ (blue curve), and the
• APPROXIMATE median $\frac23 \sigma$, plotted as a function of $\sigma$ (orange curve)

It's a nice fit - but it is not the population median. Also note that it is a constant (a function of parameter $\sigma$) ... so there is no such meaningful thing as $E[median[X]]$ in this context.

Answer 2

The constant $2/3\approx 0.66667$ in the question approximates $\Phi^{-1}(3/4) \approx 0.67449$ (the third quartile of the standard Normal distribution) as $n$ grows large. See equation $(3)$ below.

---

To avoid the nuisance of dealing with medians of even batches of numbers, let's focus on odd batches with $2n+1$ numbers, for which the middle value (the median) is the $n+1^\text{st}$ largest or smallest. When those numbers are assumed identically and independently distributed according to some continuous distribution $F$ (with density $F^\prime=f$), their median is a random variable with density

$$F_{2n+1;n}(x) = \binom{2n+1}{n,\,1,\,n}F^n(x) (1-F(x))^n f(x).\tag{1}$$

(The multinomial coefficient can be computed as $\binom{2n+1}{n,\,1,\,n} = (2n+1)!/(n!1!n!)$.)

Now suppose the numbers are the absolute values of random variables having a continuous distribution $\Phi$ symmetric around $0$. The distribution of the absolute value of such an $X$ is, by definition,

$$\eqalign{F(x) &= \Pr(|X| \le x) = \Pr(-x \le X \le x) \\&= \Pr(X \le x) - \Pr(X \lt -x) \\&= \Phi(x) - \Phi(-x) = 1-2\Phi(-x).}$$

Writing $\phi(x)$ for $\frac{d}{dx}\Phi(x)$, its density therefore is

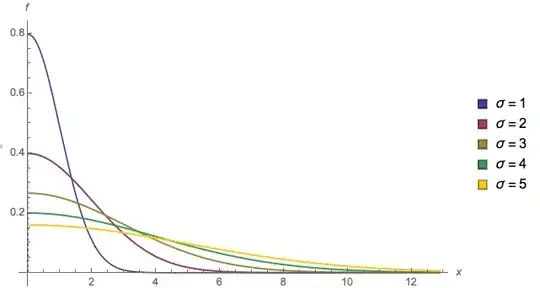
$$f(x) = \frac{d}{dx}\left(1-2\Phi(-x)\right) = 2\phi(-x) = 2\phi(x).$$

Plug this into $(1)$ to obtain the density of the median of $|X_1|, |X_2|, \ldots, |X_{2n+1}|$,

$$F_{2n+1;n}(x) = \binom{2n+1}{n,\,1,\,n}(1-2\Phi(-x))^n(2\Phi(-x))^n 2 \phi(x).\tag{2}$$

For the standard Normal distribution $\Phi$, the expectation of $(2)$--which is the integral of $xF_{2n+1;n}(x)$ from $0$ to $\infty$--has a convenient closed form only when $n=0$. For larger $n$ it can readily be numerically integrated, though, because the distribution of the median rapidly approaches Normality and its limiting mean must be the median of $|X|$ itself. That median $m_{|X|}$ satisfies

$$1/2 = F_{2n+1;n}(m_{|X|}) = 1 - 2\Phi(-m_{|X|}),$$

with the unique solution

$$m_{|X|} = -\Phi^{-1}(1/4) = \Phi^{-1}(3/4),$$

the upper quartile of the standard Normal distribution.

Computations based on $n=0, 1, \ldots, 129$ suggest a nice approximation. Let's compare the expectation, given by

$$E(n) = \mathbb{E}(\operatorname{median}(|X_1|,\ldots,|X_{2n+1}|) = \int_0^\infty x F_{2n+1;n}(x)dx$$

to its limiting value

$$\lim_{n\to\infty} E(n) = m_{|X|} = \Phi^{-1}(3/4).$$

The difference is approximately $\delta(n) = 0.1043642189 / (n+1)$; that is,

$$E(n) \approx \Phi^{-1}(3/4) + \frac{0.1043642189}{n+1}.\tag{3}$$

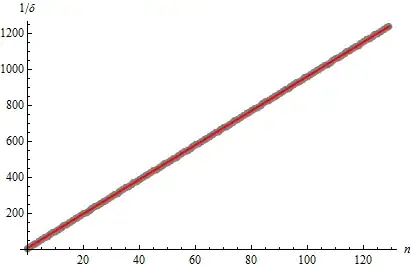
As a demonstration, here is a plot of $1/(E(n) - \Phi^{-1}(3/4))$ against $n$ for $n=0$ through $129$. The superimposed red line plots $1/\delta=9.58183(n+1)$ against $n$; the agreement is excellent.

Here are some of the residuals in this approximation. $$ \begin{array}{rlll} n & E(n) & \text{Approximation} & \text{Difference} \\ \hline \\ 0 & 0.797885 & 0.726672 & -0.0712127 \\ 10 & 0.684191 & 0.683187 & -0.0010038 \\ 20 & 0.679519 & 0.679234 & -0.0002850\\ 30 & 0.677884 & 0.677751 & -0.0001324 \\ 40 & 0.677051 & 0.676975 & -0.0000762 \\ 50 & 0.676546 & 0.676497 & -0.0000494 \\ 60 & 0.676208 & 0.676173 & -0.0000347 \\ 70 & 0.675965 & 0.675939 & -0.0000256 \\ 80 & 0.675782 & 0.675762 & -0.0000197 \\ 90 & 0.675640 & 0.675624 & -0.0000156 \\ 100 & 0.675526 & 0.675513 & -0.0000127 \\ 110 & 0.675432 & 0.675422 & -0.0000105 \\ 120 & 0.675354 & 0.675345 & -0.0000089 \\ \hline 400 & 0.6747502 & 0.6747500 & -0.0000002 \\ 1000 & 0.67459404 & 0.67459401 & -0.00000003 \\ 10,000 & 0.6745001858 & 0.6745001856 & -0.0000000003 \end{array}$$

(The final value may be imprecise.) The last three lines are extrapolations of this formula to much higher values of $n$: that they work so well suggests the constant $0.1043642189$ is accurate.

Higher-order approximations can readily be worked out.

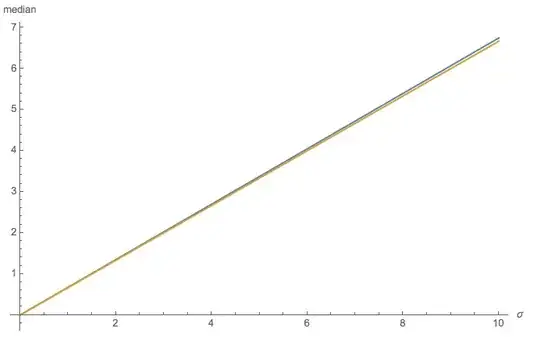
Finally, $\sigma$ is merely a scale factor for the Normal distribution and thereby will multiply $E(n)$ when the underlying distribution is Normal$(0,\sigma)$.