I want to find the optimal number of clusters (k) for some clustering algorithm (agglomerative hierarchical, if that matters). I want to evaluate the quality of clustering based on some metric for each possible cluster (k=1, 2, 3, ...). Since the number of possible k's can be as large as the number of data points, it is not practical to check the evaluation metric for each k. Therefore, if there exists a metric which when plotted against k, is independently monotonic on either side of the most "optimal" k (i.e., the k for which the metric's value is highest), then it would be possible to ask the question, "Can we reduce the search space for k?". That is, instead of evaluating the metric for all k, is it possible to identify a subset or neighbourhood where the best k is guaranteed to be present?
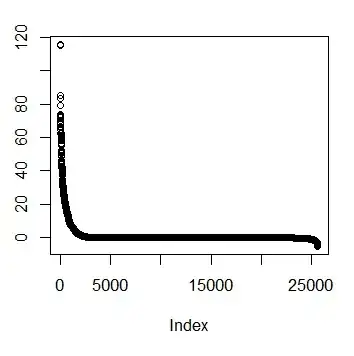
If such a metric exists, the graph would look something like this:
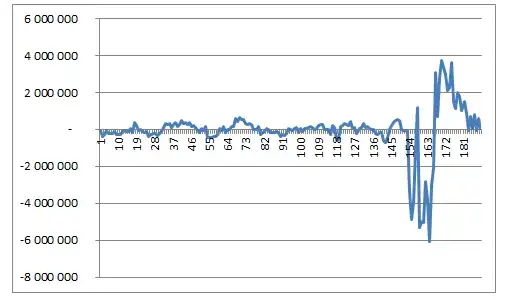
I tried different metrics that I could find by online search: C-index, Dunn index, Davies-Bouldin index, Calinski-Harabasz index, Silhouette Width. But none of them have guarantee on independent monotonicity on either side of the optimal k for ALL datasets - maybe some of them behave like this on some data, but not on other data. For example:
So, does such a metric exist? Or is it possible to construct one?