24

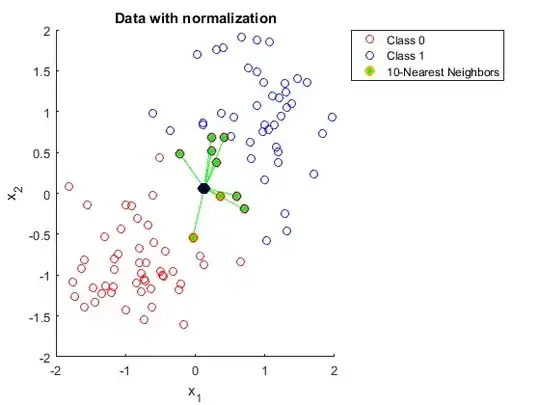
Could someone please explain to me why you need to normalize data when using K nearest neighbors.

I've tried to look this up, but I still can't seem to understand it.

I found the following link:

https://discuss.analyticsvidhya.com/t/why-it-is-necessary-to-normalize-in-knn/2715

But in this explanation, I don't understand why a larger range in one of the features affects the predictions.

bugsyb
  • 491
  • 1
  • 5
  • 13
  • I think normalization has to be justified from the subject-matter point of view. Essentially, what matters is what defines the distance between points. You have to find a convenient arithmetic definition of distance that reflects the subject-matter definition of distance. In my limited experience, I have normalize in some but not all directions based on subject-matter considerations. – Richard Hardy Jun 26 '17 at 19:00
  • 1
    For an instructive example, please see https://stats.stackexchange.com/questions/140711. – whuber Jun 26 '17 at 19:28
  • It seems like any scaling (min-max or robust) is acceptable, not just standard scaling. Is that correct? – skeller88 Apr 10 '20 at 20:20

4 Answers4

37

The k-nearest neighbor algorithm relies on majority voting based on class membership of 'k' nearest samples for a given test point. The nearness of samples is typically based on Euclidean distance.

Consider a simple two class classification problem, where a Class 1 sample is chosen (black) along with it's 10-nearest neighbors (filled green). In the first figure, data is not normalized, whereas in the second one it is.

Data without normalization Data with normalization

Notice, how without normalization, all the nearest neighbors are aligned in the direction of the axis with the smaller range, i.e. $x_1$ leading to incorrect classification.

Normalization solves this problem!

kedarps
  • 2,902
  • 2
  • 19
  • 30
  • 2
    This answer is exactly right, but I fear the illustrations might be deceptive because of the distortions involved. The point might be better made by drawing them both so that the two axes in each are at the same scale. – whuber Jun 26 '17 at 19:30
  • 1
    I found it difficult to fit all data points in the same scale for both figures. Hence, I mentioned in a note that scales of axes are different. – kedarps Jun 26 '17 at 19:55
  • 1
    That difficulty actually is the point of your response! One way to overcome it is not to use such an extreme range of scales. A 5:1 difference in scales, rather than a 1000:1 difference, would still make your point nicely. Another way is to draw the picture faithfully: the top scatterplot will seem to be a vertical line of points. – whuber Jun 26 '17 at 19:57
  • 2
    @whuber, I misunderstood your first comment. Fixed the plots, hopefully it's better now! – kedarps Jun 26 '17 at 20:10
  • @kedarps Can I ask exactly how you normalized the data? Did you just subtract the mean and divide by the standard deviation? – Undertherainbow Mar 11 '19 at 12:33
  • 1
    @Undertherainbow That is correct! – kedarps Mar 11 '19 at 19:33
  • I checked the answer before the edit and I think it was way better with the different scales. You already had the normalization visually and could see how the point _should_ be classified but at the same time you could see that the scales are different which leads to the shown nearest neighbors. I suggest going back to the initial images. – das Keks Apr 21 '21 at 13:07
9

Suppose you had a dataset (m "examples" by n "features") and all but one feature dimension had values strictly between 0 and 1, while a single feature dimension had values that range from -1000000 to 1000000. When taking the euclidean distance between pairs of "examples", the values of the feature dimensions that range between 0 and 1 may become uninformative and the algorithm would essentially rely on the single dimension whose values are substantially larger. Just work out some example euclidean distance calculations and you can understand how the scale affects the nearest neighbor computation.

Derek Jones
  • 91
  • 3
0

If the scale of features is very different then normalization is required. This is because the distance calculation done in KNN uses feature values. When the one feature values are large than other, that feature will dominate the distance hence the outcome of the KNN.

see example on gist.github.com

Ajey
  • 155
  • 4
0

The larger the scale a particular feature has relative to other features, the more weight that feature will have in distance calculations. Scaling all features to a common scale gives each feature an equal weight in distance calculations. But notice that scaling introduces a particular weighting on the distance function, so how can we assume that it is somehow the correct one for KNN? So my answer is: scaling should not be assumed to be a requirement.

JGrossman
  • 1