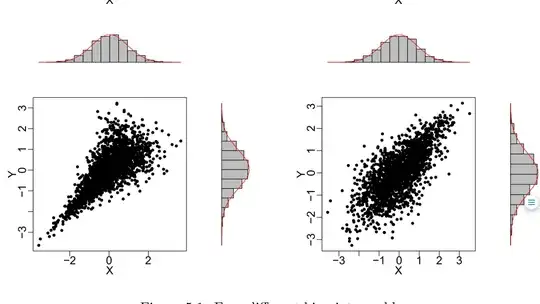
 How would I go about generating data with the same pearson's correlation, But different dependence structure as can be seen above. Basically I want to show short coming of linear correlation as a descriptive measure of dependence.
How would I go about generating data with the same pearson's correlation, But different dependence structure as can be seen above. Basically I want to show short coming of linear correlation as a descriptive measure of dependence.
Many Thanks
 How would I go about generating data with the same pearson's correlation, But different dependence structure as can be seen above. Basically I want to show short coming of linear correlation as a descriptive measure of dependence.
How would I go about generating data with the same pearson's correlation, But different dependence structure as can be seen above. Basically I want to show short coming of linear correlation as a descriptive measure of dependence.
Many Thanks