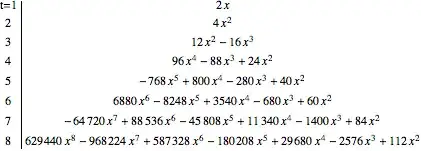Given: $X$ and $Y$ are independent standard Normals with pdf's $\phi(.)$ and cdf's $\Phi(.)$.
Since $X$ and $Y$ are independent, the joint pdf of $\big((X \; \big|\;X<c), \; Y\big)$ is $f(x,y) = {\large\frac{\phi(x)}{\Phi(c)}} \phi(y)$:
where Erf[.] denotes the error function.
Part 1: The pdf of $Z = X+Y \; | \; X<c$
Given $f(x,y)$, consider the transformation $(Z = X+Y, V=Y)$.
If $X <c$ and $Z = X+Y$, then $Z < c + Y$. That is, $Z < c + V$. This dependency is invoked in the following line using the Boole statement. Then the joint pdf of $(Z,V)$, say $g(z,v)$ can be obtained with:

... where I am using the Transform function from mathStatica/Mathematica to automate the nitty-gritties using the Method of Transformations (Jacobian etc).
The pdf of $Z$ that we seek is simply the marginal pdf of $Z$:

... which is our desired closed form solution.
The following diagram plots the pdf of $Z$ (i.e. the sum of 2 independent Normals, conditional on one of them) for six different vales of parameter $c$:
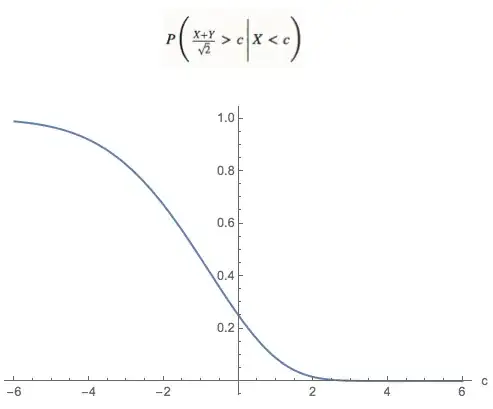
Part 2: Find $P\left(\frac{X+Y}{\sqrt{2}}>c\,\Biggl|\,X<c\right)$
To find $P\left(\frac{X+Y}{\sqrt{2}}>c\,\Biggl|\,X<c\right)$, integrate the above pdfZ over $(\sqrt2 c, \infty)$ wrt $z$.
Alternatively, $P\left(\frac{X+Y}{\sqrt{2}}>c\,\Biggl|\,X<c\right)$ can be obtained directly from the first step by :
... where I am using the Prob function from mathStatica/Mathematica to automate the nitty-gritties. This solution can be written in conventional notation as:
$$\frac{1}{\Phi(c)} \quad \int_{-\infty}^c \phi(x) \; \Phi \left(x-\sqrt{2} c\right) \, dx$$
While the probability does not appear to have a convenient closed-form, it is nevertheless a useful and practical result that is reduced to integrating a single variable. In particular:
a) when $c = 0$, the solution simplifies to $\frac14$
b) for other $c$ values, replace Integrate with NIntegrate for a solution via numerical integration in a single variable, which works very nicely. For instance, here is a plot of the desired probability, as a function of the truncation point $c$: