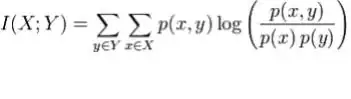Your table of "joint probabilities" is not what you assume it to be. Joint probability $\Pr(X, X)$ means probability that $X=x$ and that $X=x$. Obviously $X=x$ is the same as $X=x$, so your table should have entries only on the diagonal. To prove it to ourselves, let's simulate:
X <- sample(1:3, 1000, replace = TRUE, prob = c(1, 5, 2))
prop.table(table(X, X))
## X
## X 1 2 3
## 1 0.137 0.000 0.000
## 2 0.000 0.595 0.000
## 3 0.000 0.000 0.268
From your comment it seems that you misunderstand the general ideas (or notation) used in probability theory. Then we are talking about $\Pr(X=x)$ we mean probability that random variable $X$ takes value $x$, where $x$ stands for some particular value.
To make this more concrete, take one coin out of your wallet. This coin is not random, it is actually far from being random as it is very fixed metal object. What we consider as random, is the outcome of experiment, where we will be tossing this coin. It is random because, before we toss it, the outcome of such experiment is uncertain and unpredictable for us. Let's call the experiment of tossing this coin once as $A$. It potentially can have two outcomes: heads or tails ($h_A, t_A$ for simplicity). Now, when we are talking about $\Pr(A = h_A)$ we mean probability that in our experiment we will observe heads. Now imagine that we have two coins, and we toss them simultaneously. $\Pr(A = h_A, B = h_B)$ is the probability of observing heads in experiment $A$ and heads in experiment $B$. We may consider different experiments, e.g. let's toss the first coin two times and call outcome of the first toss as $A_1$, and outcome of the second toss as $A_2$. Now $\Pr(A_1 = h_{A_1}, A_2 = t_{A_2})$ is the probability that in the first toss we observed heads and in the second toss we observed tails. Notice that we used a single coin, but we denoted outcomes of the two experiments as two distinct random variables.
What follows, $\Pr(X = x, X = x)$ is the probability that when in the next few minutes you will toss the coin, that you took out of your wallet, it will land heads and that it will land heads, so it's a tautology. It is impossibility for $X$ to take two different values at the same time.
See also the joint distribution of x with..itself thread that extends this case to probability density functions.