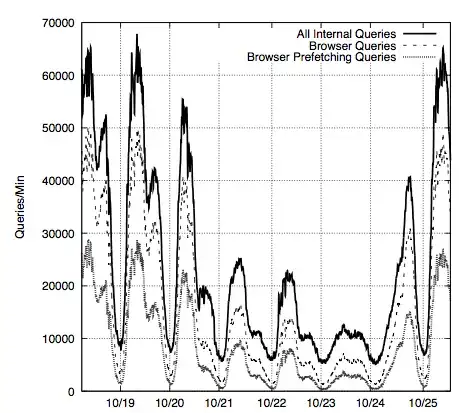
I have data sets of network traffic that exhibit strong diurnal effects making them non-stationary. One of the analysis that I want to run is to show correlation between days. If we chopped up the time series into individual days, how would I
- ...show the individual time series are stationary? Would applying Augmented Dickey-Fuller be enough?
- ...perform cross-correlation? Would computing Pearson's be enough?
The next step is to check for long range dependence. This a tougher challenge since I can not chop up the time series into individual days. Any ideas?
The final question is in reference to the figure I am attaching, the 3 time series on that figure are non-stationary. I want to check for correlation, should I use chop them into smaller hourly/daily time series or apply a decomposition method. I am not too familiar with detrending or differencing methods. Any pointers would be great.