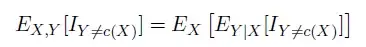pipes vs commas in expectation notation subscript

Question

Sorry if this is a really basic question as I am new to the field.

My question builds off of another question "subscript notation in expectations" found here, but that question does not address pipes or commas in the subscript: Subscript notation in expectations

This question is very similar but the author basically just asks if their math is correct, so there is no explanation like what I'm hoping for: Conditional expectation subscript notation

So, on to my question. In the below equation, how should we interpret the meaning of the commas and pipes in the subscripts? I am guessing that the pipes indicate conditional expectation, but I'm not sure what to think about the commas.

As background, the equation is discussing classification error. I is an indicator function and c is a classifier. I believe that I and its subscript would be read as, "an indicator function that is true when the classifier c(X) is not equal to Y, i.e. when the classifier is wrong."

It is taken from the ML paper "Training Highly Multiclass Classiers" by Gupta, Bengio, and Weston. http://jmlr.org/papers/v15/gupta14a.html (bottom of page 1463)

Answer 1

What you call pipes are actually vertical bars (for best results, use \mid rather than \vert in LaTex), and these bars denote conditioning: $P(A\mid B)$ is the conditional probability of the event $A$ conditioned on $B$ having occurred. The commas are unfortunate usage when it comes to expectations. The law of iterated expectation (LIE) says that $E[Y] = E\left[E[Y\mid X]\right ]$ where the inner $E$ is the conditional expectation of $Y$ given $X$, and in spite of its appearance, it ($E[Y\mid X]$) is a function of $X$, not of $Y$. The outer $E$ is the expectation of $E[Y\mid X]$ which is a function of $X$, not $Y$, remember? and the big fat LIE here is that the numerical value of the expectation of $E[Y\mid X]$, a function of $X$, by a miracle of modern mathematics, just happens to equal $E[Y]$, the expectation of $Y$. In your parlance, this would read $$E_{X,Y}[Y] = E_X\left [E_Y[Y\mid X]\right]$$ where the $E_Y$ is a reminder that the expectation is being computed is with respect to $Y$ (with $X$ being treated as a constant as far as expectations are concerned, which is why $E[Y\mid X]$ is a function of $X$, not of $Y$: we have no more expectations from $Y$). The $E_X$ is a reminder that the thingie we are computing the expectation of is a function of $X$ and so we compute the expectation with respect to $X$. finally, that $E_{X,Y}$ on the left is a reminder that when we are computing the expectation of $Y$ and we know that there is another variable $X$ floating around there somewhere, then we need to use something like $$E[Y] = \int\int y \cdot f_{X,Y}(x,y)\,\mathrm dx \, \mathrm dy$$ in computing the expectation. Of course, the double integral can also be re-written as $$\int y \cdot \left[ \int f_{X,Y}(x,y)\,\mathrm dx \,\right ] \mathrm dy = \int y \cdot f_{Y}(y)\,\mathrm dy.$$

---

In your specific case, we have a new variable $Z = \mathbf 1_{Y \neq cX}$ which is a function of both $X$ and $Y$, and so $$E[Z] = E\left[ E[Z \mid X] \right ]$$ or more prolixly, $$E_{X,Y}[Z] = E_X\left [E_Y[Z \mid X]\right]$$ is how one should write it. Contrary to an oft-expressed belief on this site, there is no random variable called $Y\mid X$ abd so $E_{Y\mid X}$ makes no sense to me. But YMMV.