1

Say I see a bimodal distribution like this (with the domain, or random variable, $Z$):

enter image description here

Does that instantly mean that I am seeing not a distribution of one independent random variable $Z$, but actually a composite of two distributions (associated with two truly independent random variable $X$ and $Y$), even though $X$, $Y$ and $Z$ all have the same range $[-6,6]$?

In this instance the figure above was obtained by: $$P_{Z} = 0.5 \cdot P_{X} + 0.5 \cdot P_{Y} $$

enter image description here

enter image description here

As an example, say that $Z$ is height. Does it mean that from a probability perspective $Z$ is actually two mathematically distinct (despite the name) variables female height and male height?

A.L. Verminburger
  • 176
  • 1
  • 10
  • 1
    If you see it in empirical data, especially with small sample size, thie may mean simply that you have noisy data... – Tim Jun 09 '17 at 13:27
  • @Tim I am seeing this in empirical data large enough to consider it a good approximation of a true random variable (if it was unimodal). – A.L. Verminburger Jun 09 '17 at 13:57
  • 1
    I believe my answer at [Why are all known distributions unimodal?](https://stats.stackexchange.com/questions/91537) provides a thorough analysis of this situation from a theoretical point of view. It proves that *all multimodal distributions are mixtures of unimodal distributions.* The proof makes it clear that the decomposition into a mixture is not unique. Are you perhaps asking the empirical question, "when I see an empirical mixture distribution should I (at least in principle) be able to find a categorical covariate that identifies each component?" – whuber Jun 09 '17 at 15:12
  • 1
    @whuber If there exists a mathematical proof that all multimodal distributions can be decomposed into unimodal distributions, that, I believe, would effectively answer my question as "correct" (and it is a mathematical, rather than an empirical justification I was mostly after). – A.L. Verminburger Jun 09 '17 at 15:30
  • @A.L.Verminburger A unimodal distribution can also be decomposed into a mixture of two variables. Therefore, I don't see why a bimodal distribution would be any more indicative of a mixture of two variables than a unimodal one (I mean, I "see" why, but I'm not sure it can bet set apart formally). – cangrejo Jun 09 '17 at 15:52
  • @broncoAbierto I am assuming decomposition holds. I see how unimodal could be composed of two similar (mean being the same, but different variance if talking about normal-like distributions). It is a difficult case -- will look like one unimodal. But if it is multimodal (and the modes are of different heights) [sorry for the "soft" non-mathematical description] the "variables" are arguably more distinct, the distinction being both in means and variances (again thinking about normal-like variables). – A.L. Verminburger Jun 09 '17 at 16:05
  • @whuber I would not say the questions are duplicate. The questions are different. It just happens that an answer to one may also be an answer to the other: a one-to-many relationship. E.g. "what is the colour of the sun? -- yellow; what is the colour of lemons? -- yellow": same answer, but different questions. – A.L. Verminburger Jun 09 '17 at 16:11
  • When questions are phrased differently, but have identical answers, they are usually considered duplicates. The process of closing, *but not deleting*, the duplicates provides a systematic way for people to find a question through the site search: each new phrasing of the same question enhances their chances to find that common answer. There are subtleties and some controversy: for instance, when it requires a nontrivial mathematical operation to transform one question into another, they are often considered different. But that's not the case here. – whuber Jun 09 '17 at 17:44

1 Answers1

3

Perhaps you should revisit the definitions of random variable and distribution to clarify things. For random variables, I like the one on Wikipedia for its simplicity.

A random variable $X : \Omega \rightarrow E$ is a measurable function from a set of possible outcomes $\Omega$ to a measurable space $E$.

On the other hand, the cumulative distribution function $F_Z$ of a random variable $Z$, as you know, represents the probability that $Z$ takes a value within a specific region, that is, $F_Z(x)=Pr(Z\leq x)$.

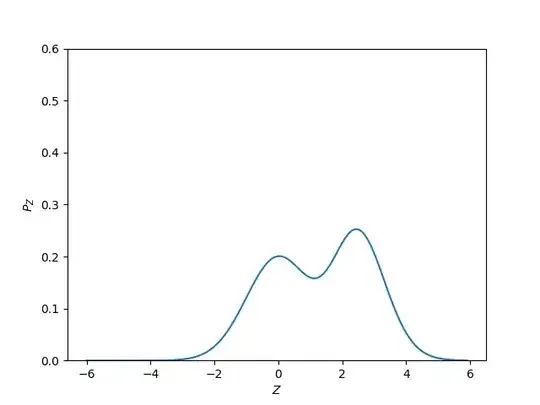
The probability density function $f_Z$ of $Z$, that is, your first plot, can be defined simply as $$ f_Z(x)=\frac{d}{dx}F_Z(x) $$ And of course, $F_Z$ is such that $\lim_{x\rightarrow \infty}\int_{-\infty}^x f_Z(x)dx=1$

Therefore, for any continuous random variable, we can come up with whichever density we want, provided it is nonnegative and intregrates to $1$. It can have one, two, four or infinitely many modes, and the corresponding random variable can be represented as a single variable or as a mixture of infinitely many, differently distributed, variables.

So, are two modes indicative of two variables? That's up to you. You should propose a mixture model for your data if you feel that is consistent with your understanding of the phenomena behind them.

But are two modes indicative of two random variables? Well, just bear in mind that that is a well-defined mathematical concept, so you just need to go the definition to see what you can take for granted and what not (no, the answer is no).

cangrejo
  • 2,121
  • 13
  • 22
  • I am familiar with the axioms of probability. You are saying that according to them there is no restriction for a single continuous random variable to have a bimodal distribution. If that is the case, why do we not have a single standard bimodal distribution (https://en.wikipedia.org/wiki/Univariate_distribution)? Multimodality therefore seems to me indicate that the random variable is not pure and can be "factored out". – A.L. Verminburger Jun 09 '17 at 14:50
  • Isn't the uniform distribution multimodal? – cangrejo Jun 09 '17 at 14:53
  • The point is that you can define any distribution you want, at least formally. There are thus infinitely many possible distributions. The distributions that have names are simply cases that have been discovered to have some interesting properties, or that are useful for analyzing real-world phenomena. We tend to see multimodal or otherwise complex shapes as mixtures because it is often easier to work with well-known distributions, rather than arbitrary models. – cangrejo Jun 09 '17 at 15:09
  • I would imagine that with some exception (exponential or uniform) most variables found in the natural world would have a unimodal distribution (as it encapsulates the notion of low or high value relative to the average). Given the event that in 200 years the established distributions are predominantly unimodal, the probability of event that a bimodal distribution is actually indicating the presence of two variables would be pretty high. I do take your point mathematically (which is what I was asking for) there is no constraint on that as far as existing axioms go. – A.L. Verminburger Jun 09 '17 at 15:21
  • I guess it's down to a philosophical discussion of what one understands by "variable", but yes, in most cases, when dealing with data coming from some natural experiment, it appears to be most reasonable to divide bimodal data into two groups with some distinctive characteristic (other than having different modes!). – cangrejo Jun 09 '17 at 15:42
  • True, especially given the fact that the name "random variable" is already fuzzy given it can be seen as a function mapping events to real numbers. I would argue that what we call "random variables" are actually just non-cumulative distribution functions (which already contain the set of values $X$,which we mathematically refer to as the random variable, in the domain). We can have two random variables (which really are just finite or infinite sets as far as I understand in the traditional definition, event if includes raw non-mapped events),which are identical (but have different distribs.). – A.L. Verminburger Jun 09 '17 at 15:57