I know that from Hastie et. al's paper, that in the single response $y$ LASSO, the $\lambda$ values are chosen such that: $N\alpha\lambda_{max} = \max_l |< x_l, y_l > |$ Also, $y$ is by default standardised before forming the grid of $\lambda$ values on log-scale. Then, the grid is de-standardized by multiplying back by $\sigma_y$.
I'm trying to understand how this is done if $Y$ becomes a matrix (i.e multiresponse). Any ideas how $\lambda$ would then be formed?
Short answer for the simplest case (no intercept, no standardization)
library(glmnet)
set.seed(125)
n <- 50
p <- 5
k <- 2
X <- matrix(rnorm(n * p), ncol=p)
y <- matrix(rnorm(n * k), ncol=k)
max(glmnet(X, y, family="mgaussian",
standardize = FALSE,
standardize.response = FALSE,
intercept=FALSE)$lambda)
max(sqrt(rowSums(crossprod(X, y)^2))/n)
If you want to add intercept handling / standardization of $X$ and/or $y$, see discussion elsewhere on this site.
So where does this come from?
Let's review the standard lasso case first:
$$\text{arg min}_{\beta} \frac{1}{2n} \|y - X\beta\|_2^2 + \lambda \|\beta\|_1$$
The stationarity condition from the KKT conditions says that we must have
$$ 0 \in \frac{-X^T}{n}(y-X\beta) + \lambda \partial \|\beta\|_1 $$
The first term on the RHS is just the gradient of the smooth $\ell_2$-loss; the second term is the so-called subdifferential of the $\ell_1$-norm. It arises from an interesting alternate characterization of derivatives for convex functions which can be extended to non-smooth case quite easily. (See below for some details) For now, it's sufficient to know that it's a set of numbers and we need 0 to be in that set at the solution.
We are interested in the case where $\beta = 0$. In this case, the subdifferential of the absolute value function $\partial |\beta|_{\beta = 0}$ is the set $[-1, 1]$, so the subdifferential of the vector $\ell_1$-norm is $\partial \|\beta\|_1 = [-1, 1]^p$. That is, the set of all vectors in the $p$-dimensional hypercube.
Hence, we need to be able to find some $s \in [-1, 1]^p$ satisfying $$0 = -\frac{X^Ty}{n} + \lambda s$$ for $\beta = 0$ to be a solution. Rearranging, we get $$\frac{X^Ty}{n} = \lambda s$$
This is a set of vector equations with $p$ elements on each side, so let's look at just the first one:
$$\frac{(X^Ty)_1}{n} = \frac{X^T_1 y}{n} = \lambda s_1$$
We know that $s_1$ is in $[-1, 1]$, so $\lambda s_1$ is in $[-\lambda, \lambda]$. Hence, for this equation to hold, we must have $|X^T_1y/n| \leq \lambda$.
By symmetry, this must hold for all $i$, so we have $\max |X^T_iy/n| = \|X^Ty/n\|_{\infty} \leq \lambda$. Taking the smallest $\lambda$ that satisfies this equation, we get
$$\lambda_{\max} = \left\|\frac{X^Ty}{n}\right\|_{\infty}$$
Now, let's consider the group lasso penalty for the multi-response Gaussian, defined as
$$\text{arg min}_{B} \frac{1}{2n}\|Y - XB\|_2^2 + \lambda \|B\|_{1, 2}$$
where $Y \in \mathbb{R}^{n \times k}, X \in \mathbb{R}^{n \times p}$, and $B \in \mathbb{R}^{p \times k}$ and the penalty $\|B\|_{1, 2}$ is the $\ell_1/\ell_2$-mixed norm given by
$$ \|B\|_{1, 2} = \sum_{i=1}^p \|B_i\|_2 = \sum_{i=1}^p \sqrt{\sum_{j=1}^k B_{ij}^2} $$
We can do an analysis like before, but here we need the subdifferential of the $\ell_1/\ell_2$-mixed norm. It can be shown (below) that it is given by the $p$-fold Cartesian product of unit-or-smaller $k$ vectors.
As before, we get:
$$\frac{(X^TY)_i}{n} = \lambda s_i$$
except here the LHS is a $k$ vector and $s_i$ is a unit-or-smaller $k$ vector. Since $s_i$ is a unit vector, for there to be any solution, we must have $\|(X^TY)_i/n\|_2 < \lambda$. Again, taking the max over all $i$, we get $$\max_i \|(X^TY)_i/n\|_2 = \|X^TY/n\|_{\infty, 2} \leq \lambda$$ so $$ \lambda_{\max} = \|X^TY/n\|_{\infty, 2}$$
This is what we calculated above as max(sqrt(rowSums(crossprod(X, y)^2))/n).
So where does this all come from? Let's start by noting an important fact about convex functions: their Taylor series under-estimate them. That is, if $f$ is sufficiently smooth and convex, then the Taylor expansion of $f$ around $x$:
$$\tilde{f}_x(y) = f(x) + f'(x)(y-x)$$
will underestimate $f$:
$$ \tilde{f}_x(y) \leq f(y), \quad \forall x, y $$
This follows from Taylor's remainder theorem which says that the error will be of the form $f''(x)(y-x)^2/2$ - if $f$ is convex, then we have $f''(x) \geq 0$ everywhere, hence the Taylor series underestimates.
If we turn this around, we can say that for a convex function $f$, we can find $c$ such that
$$\tilde{f}_x(y) = f(x) + c(y-x)$$
Any $c$ satisfying this is called a subgradient of $f$ at $x$ and the set of all such $c$ is called the subdifferential of $f$ at $x$. If $f$ is differentiable, then there is only one subgradient which is just the gradient (and the subdifferential is just a set with one element), but if $f$ is not differentiable, then there are multiple possible subgradients (and hence a large subdifferential).
The classic example is $f(x) = |x|$, which is clearly non-differentiable at $0$. It is easy to see that any $c \in [-1, 1]$ is a subgradient:
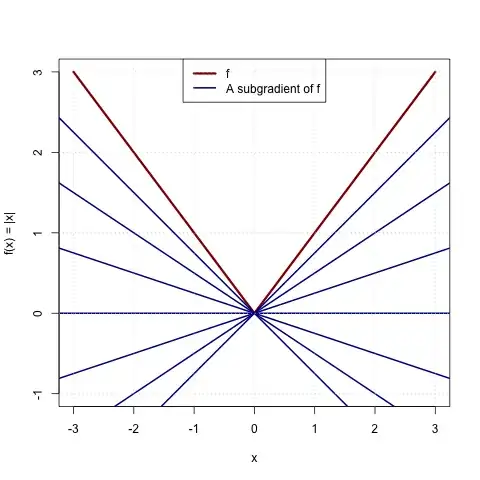
Any of the blue lines (Taylor-type approximations using a subgradient) are everywhere below the red line (the function).
For the general $\ell_1$ norm on $\mathbb{R}^p$, it's not hard to see that the subdifferential is just the $p$-fold Cartesian product of the univariate subdifferential since the $\ell_1$-norm is separable across entries.
If we want to consider more general norms (e.g., the mixed $\ell_{1, 2}$ norm), we can invoke a more general theorem characterizing the subdifferential of norms.
Let $\|\cdot\|$ be a general norm. Then its subgradient is given by
$$\partial \|x\| = \{v : v^Tx = \|x\|, \|v\|_{*} \leq 1\}$$
where $\|v\|_{*} = \max_{z: \|z\| \leq 1} v^Tz$ is a different norm called the dual norm to $\|\cdot\|$. Evaluated at $x = 0$, we see that the subdifferential is the set of all vectors with dual norm at most 1.
One direction of the proof is easy: suppose $v$ is an element of the RHS above. Then consider the Taylor type expansion of $f(\cdot) = \|\cdot\|$ around $x$ evaluated at $y$ with (potential) subgradient $v$:
$$\begin{align*} \tilde{f}_x(y) &= \|x\| + v^T(y - x) \\ &= \|x\| + v^Ty - v^Tx \\ & = v^Ty + \underbrace{\|x\| - v^Tx}_{=0 \text{ by assumption on $v$}} \\ &= v^Ty \\ & \leq \|v\|_*\|y\| \quad \text{(Holder's Inequality)} \\ &= \|y\|\end{align*}$$
so $v$ is indeed a subgradient of $f$.
Hence, finding the subdifferential reduces to calculating the dual norm. Fortunately, dual norms are exceptionally useful and hence well-studied. The simplest case is the standard $\ell_p$ norms where it can be shown that the dual of the $\ell_p$-norm is the $\ell_{p^*}$-norm where $p^*$ is the so-called Holder conjugate of $p$ and satisfies $1/p + 1/p^* = 1$.
For the $\ell_1$-case, $p=1$ and so $1/p + 1/p^* = 1 \implies 1/p^* = 1 - 1/1 = 0 \implies p^* = \infty$. Hence the subgradient is just the set of vectors with $\|v\|_{\infty} \leq 1$, which is exactly the set $[-1, 1]^p$ we claimed above.
For mixed-norms, the result is almost as easy. See Lemma 3 of [Sra12] for a proof of the fact that the dual of the $\|\cdot\|_{p, q}$ mixed-norm is simply $\|\cdot\|_{p^*,q^*}$ where $p^*,q^*$ are the Holder conjugates of $p, q$ respectively.
We hence note that the dual of the $\|\cdot\|_{1, 2}$ norm used for the group lasso is $\|\cdot\|_{\infty, 2}$ (because $1/2 + 1/2 = 1$) which has an associated unit ball which is the $p$-fold Cartesian product of vectors with Euclidean ($\ell_2$) norm at most 1, as claimed above.
[Sra12] "Fast projections onto mixed-norm balls with applications" Suvrit Sra. ArXiv 1205.1437
sorry I'm new to the community, still trying to get the hang of it! Thank for editing my question @F. Tusell. The link to the original article came from: https://web.stanford.edu/~hastie/Papers/glmnet.pdf.
But the paper did not mention much about what was done regarding multi-variate response. The vignette for the R package glmnet (link: https://web.stanford.edu/~hastie/Papers/Glmnet_Vignette.pdf), on page 17, explained how the objective function looked like, incorporating the group LASSO penalty. But, I can't seem to be able to reproduce value of lambda_max used to form the grids.
