10

I was experimenting with the relationship between the errors and the residuals using some simple simulations in R. One thing I've found is that, regardless of the sample size or error variance, I always get exactly $1$ for the slope when you fit the model

$$ {\rm errors} \sim \beta_0 + \beta_1 \times {\rm residuals} $$

Here's the simulation I was doing: 

n <- 10 
s <- 2.7 

x <- rnorm(n) 
e <- rnorm(n,sd=s)
y <- 0.3 + 1.2*x + e

model <- lm(y ~ x) 
r <- model$res 

summary( lm(e ~ r) )

e and r are highly (but not perfectly) correlated, even for small samples, but I can't figure out why this automatically happens. A mathematical or geometric explanation would be appreciated.

GoF_Logistic
  • 230
  • 2
  • 9
  • 5
    In the plane triangle OXY, with base OX, the altitudes of the sides YO and XY are the altitude of the triangle itself. In order, those altitudes are given by the coefficients of `lm(y~r)`, `lm(e~r)`, and `lm(r~r)`, which therefore must all be equal. The latter obviously is $1$. Try out all three of these commands to see. To make the last one work in `R` you have to create a copy of `r`, such as `s – whuber Jun 06 '17 at 15:34
  • 1
    Thanks @whuber. Would you like to make than an answer so I can accept it, or perhaps mark this as a duplicate? – GoF_Logistic Jun 06 '17 at 16:59
  • 1
    I don't think it's a duplicate, so I have expanded the comment into an answer. – whuber Jun 06 '17 at 18:18

2 Answers2

11

Without any loss of conceptual (or practical) generality, first remove the constant from the variables as described at How exactly does one "control for other variables". Let $x$ be the regressor, $e$ the error, $Y=\beta x + e$ the response, $b$ the least-squares estimate of $\beta$, and $r = Y - bx$ the residuals. All of these vectors lie in the same plane, allowing us to draw pictures of them. The situation can be rendered like this, where $O$ designates the origin:

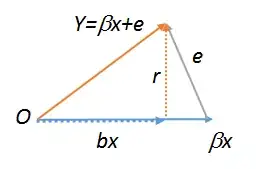
Figure

This picture was constructed beginning with $\beta x$, then adding the error $e$ to produce $Y$. The altitude was then dropped down to the base, meeting it at the least-squares estimate $bx$. Clearly the altitude is the residual vector $Y-bx$ and so has been labeled $r$.

The base of the triangle is parallel to the regressor vector $x$. The altitudes of the sides $OY$ and $(\beta x)Y$ are the altitude of the triangle itself. By definition, the residual $r$ is perpendicular to the base: therefore, distances away from the base can be found by projection onto $r$. Thus the triangle's altitude can be found in any one of three ways: regressing $Y$ against $r$ (finding the height of $Y$); regressing $e$ against $r$ (finding the height of $e$), or regressing $r$ against $r$ (finding the height of $r$). All three values must all be equal (as you can check by running these regressions). The latter obviously is $1$, QED.

For those who prefer algebra, we may convert this geometric analysis into an elegant algebraic demonstration. Simply observe that $r$, $e=r+(\beta-b)x$, and $Y=e+\beta x = r + (2\beta-b)x$ are all congruent modulo the subspace generated by $x$. Therefore they must have equal projections into any space orthogonal to $x$, such as the one generated by $r$, where the projection of $r$ has coefficient $1$, QED. (Statistically, we simply "take out" the component of $x$ in all three expressions, leaving $r$ in each case.)

whuber
  • 281,159
  • 54
  • 637
  • 1,101
11

whuber's answer is great! (+1) I worked the problem out using notation most familiar to me and figured the (less interesting, more routine) derivation may be worthwhile to include here.

Let $y = X \beta^* + \epsilon$ be the regression model, for $X \in \mathbb{R}^{n \times p}$ and $\epsilon$ the noise. Then the regression of $y$ against the columns of $X$ has normal equations $X^T\left(y - X \hat\beta\right) = 0,$ yielding estimates $$\hat\beta = \left(X^T X \right)^{-1} X^T y.$$ Therefore the regression has residuals $$r = y - X \hat\beta = \left( I - H \right) y = \left( I - H \right) \epsilon,$$ for $H = X (X^T X)^{-1} X^T$.

Regressing $\epsilon$ on $r$ results in an estimated slope given by \begin{align*} (r^T r)^{-1} r^T \epsilon & = \left( \left[ \left(I - H\right) \epsilon \right]^T \left[ \left(I - H\right) \epsilon \right] \right)^{-1} \left[ \left(I - H\right) \epsilon \right]^T \epsilon \\ & = \frac{\epsilon^T \left( I - H \right)^T \epsilon}{\epsilon^T \left( I - H \right)^T \left( I - H \right) \epsilon} \\ & = \frac{\epsilon^T \left( I - H \right) \epsilon}{\epsilon^T \left( I - H \right) \epsilon} \\ & = 1, \end{align*} since $I-H$ is symmetric and idempotent and $\epsilon \not\in \mathrm{im}(X)$ almost surely.

Further, this argument also holds if we include an intercept when we perform the regression of the errors on the residuals if an intercept was included in the original regression, since the covariates are orthogonal (ie $1^T r = 0$, from the normal equations).

user795305
  • 2,692
  • 1
  • 20
  • 40