When researching the reciprocity failure (a feature of film photography, otherwise more appropriate to https://photo.stackexchange.com/) I have run into a statistical issue.
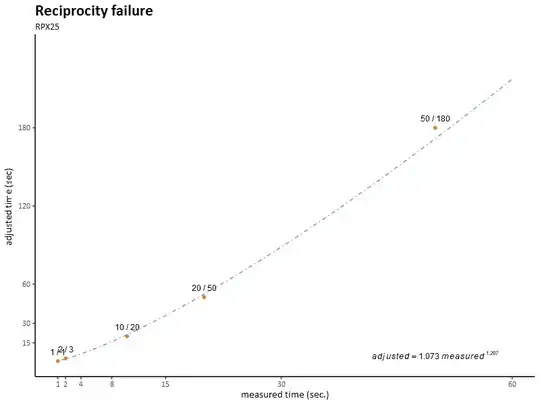
I have a datasheet for a photography film specifying the measured and effective exposure time for 5 exposure times. I found these times highly inconvenient (by convention the exposure times in photography go in powers of two - 1 second, 2, 4, 8, and then 15, 30 and 60 seconds to make a round number). As a result I set out to extrapolating my own values.
When I tried a number of possible regressions in RStudio I found the best fit with a power function.
My problem is that I am aware that 5 data points make a very small data set (but that is all that I have). I am not comfortable throwing various functions at it until something sticks.
Is there a general rule / a piece of advice when a power function is appropriate, and when a different function - such as exponential (which in my case seemed a poor fit) - would be a better choice?