There were many similar questions on this site , related to this but none were exactly to the point I wanted to ask
So the question is relates to ridge regression and This link where there is a statement(in bold) that
In a least squares fit where coefficient estimate given by
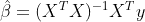
has no unique solution when 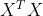 is not invertible but
is not invertible but
Inclusion of λ makes problem non-singular even if 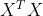 is not invertible
is not invertible
This was the original motivation for ridge regression (Hoerl and Kennard, 1970)
ie. 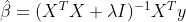
I am unable to exactly convince myself why this would be the case. Specifically for the case when p(predictors)>n(instances) how will I be able to obtain a unique solution with this?