I'm currently revising for an exam and I don't understand one of the questions. Given are the following expectation / mean vectors and covariance matrices:
A) $\mu_1 = \begin{pmatrix}0 \\ 0 \end{pmatrix}, \Sigma_1 = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix}$
B) $\mu_2 = \begin{pmatrix}3 \\ 2 \end{pmatrix}, \Sigma_2 = \begin{pmatrix} 4 & 0 \\ 0 & 1\end{pmatrix}$
C) $\mu_3 = \begin{pmatrix}3 \\ 2 \end{pmatrix}, \Sigma_3 = \frac{1}{\sqrt{10}}\begin{pmatrix} 1 & -3 \\ 3 & 1\end{pmatrix}\begin{pmatrix} 4 & 0 \\ 0 & 1\end{pmatrix}\frac{1}{\sqrt{10}}\begin{pmatrix} 1 & -3 \\ 3 & 1\end{pmatrix}^T$
where the 3rd covariance matrix is in the form $UDU^T$. We must then use this to draw the scatter diagram, as shown below
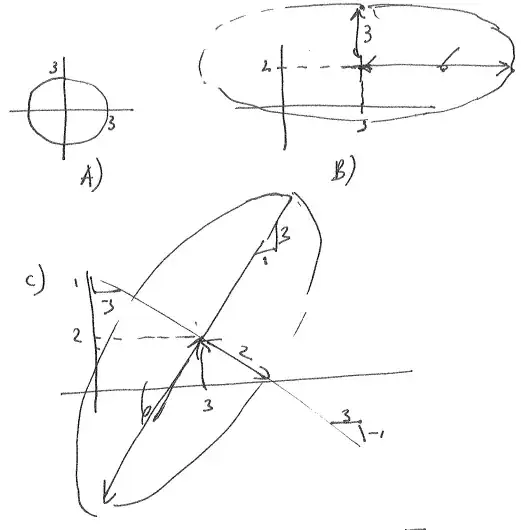
I don't understand this at all. Why is the radius for $A$ 3 and not 1? Why are the $B$ and $C$ drawn like they are? The only part I understand is that the center of the ellipse/circle is the expectation/mean vector and that the eigenvectors should be used (but not how)...