Predicting the observations in a POMDP with a recurrent neural network

Question

I use neural networks for online sequence prediction. The performance of LSTM in this case, however, is not nearly as good as I expected. Maybe someone can help me understand where the problem lies.

The peculiarity of online learning is that there is no test data set because the underlying sample distribution is allowed to be non-stationary. To be able to rapidly adapt to changes in this distribution, the model is updated each time step with the last observation as the input and the current observation as the target.

An example application is an agent that moves randomly in a grid world like the one below where the agent is currently at position (6, 2).

  0 1 2 3 4 5 6 7
0 x x x x x x x x
1 x . . . . x . x
2 x . x x . x a x
3 x . x . . . . x
4 x x x . x . . x
5 x . . . x x x x
6 x . x . . . . x
7 x x x x x x x x

The agent perceives the four cells that surround it as well as its own movement to the north, east, south, or west. An example input to the model, therefore, consists of the agent's observation of the surrounding walls (i.e., [0, 1, 0, 1] for walls to the left and the right) as well as the action performed in this situation, let's say a movement to the north (i.e., [1, 0, 0, 0]). (This is a partially observable Markov decision process.)

The resulting input vector to the model is the concatenation of the sensor and the motor encoding (i.e., [0, 1, 0, 1, 1, 0, 0, 0]). If the agent performs a movement to the north at position (6, 2), the next observation is walls everywhere, except to the south (i.e., [1, 1, 0, 1]). One training sample from the grid world above, therefore, is (input: [0, 1, 0, 1, 1, 0, 0], target: [1, 1, 0, 1]).

In each time step t:
  receive new observation o_t
  train the model with input o_{t-1} + a_{t-1} and target o_t
  randomly select new action a_t
  use o_t + a_t as input to predict the next observation o_{t+1} 

According to my understanding, the ambiguity of moving north from position (6, 2), on the one hand, and moving north from a position that appears identical to the agent (e.g. (3, 4)), on the other, should be at least partly resolvable by networks with a recurrent layer that maintains information from prior inputs.

At least, I thought, the prediction performance of a recurrent neural network should be better than a predictor based only on whatever observation followed most frequently after a particular observation-action-pair (with no regard for the prior sequence of observation-action-pairs).

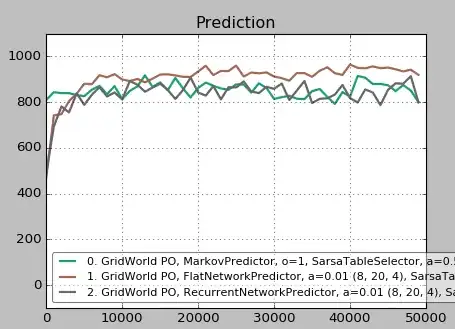
In fact, however, LSTM is merely equivalent to the predictive performance of a naive frequentist approach. A simple feedforward network with 20 neurons in one hidden layer performs better than a LSTM with the same structure.

The brown plot is the feedforward network, the black is the LSTM, and the green is a frequentist Markov predictor. The values are averaged over ten runs, each point shows the number of successful predictions over 1000 steps, and a total of 50000 steps have been performed.

Can someone assist me in understanding why this is the case?

PS: I took care to maintain the activation of the recurrent neurons throughout the process. In case, anyone's interested, here is my code for the LSTM in Keras.

import numpy
from keras.layers import Dense, LSTM
from keras.models import Sequential
from keras.optimizers import Adam


class LSTMPredictor:
  def __init__(self, observation_pattern_size: int, action_pattern_size: int, alpha: float = .01):
    self.input_size = observation_pattern_size + action_pattern_size
    self.output_size = observation_pattern_size
    self.alpha = alpha
    self.network = Sequential()
    self.network.add(LSTM(20, batch_input_shape=(1, 1, self.input_size, activation="sigmoid"), stateful=True, return_sequences=True))
    self.network.add(Dense(self.output_size, activation="sigmoid"))
    self.network.compile(loss='mse', optimizer=Adam(lr=self.alpha))

  def perceive(self, sensorimotor_pattern: Sequence[float], sensor_pattern: Sequence[float]):
    _input = numpy.reshape(sensorimotor_pattern, (1, 1, self.input_size))
    _target = numpy.reshape(sensor_pattern, (1, 1, self.output_size))
    self.network.fit(_input, _target, batch_size=1, epochs=1, verbose=0)

  def predict(self, sensorimotor_pattern: Sequence[float]) -> Sequence[float]:
    _input = numpy.reshape(sensorimotor_pattern, (1, 1, self.input_size))
    _output = self.network.predict(_input)
    return list(numpy.reshape(_output, self.output_size))

Answer 1

I think that perhaps the differences in prediction performance you are getting are just due to random fluctuations. The advantage of an LSTM over a feedforward network lies in it’s ability to remember past inputs and include them into the computation of predictions. The degree to which this yields an actual advantage depends on the number of contradictions present in the training data that can be remedied by the memory of the LSTM.

To better understand the problem I suggest to create additional grid worlds, i.e. input data, with the following properties:

1. A world (which may be similar to the one you already have) with very few or no contradictions where almost all or all predictions can be correctly determined by looking at the current input. Here, the LSTM should have almost no advantage over a feedforward network.

2. A world where almost no decision can be correctly determined by just looking at the current input, i.e. for almost all inputs looking at previous inputs is required in order to derive a correct prediction. Here, the LSTM should have a significant advantage over a feedforward network.

Additionally, I suggest employing some form of statistical test (e.g. a Friedman test) to find out whether or not the deviations of the predictions of the different models you observe are due to random effects or are actually statistically significant.