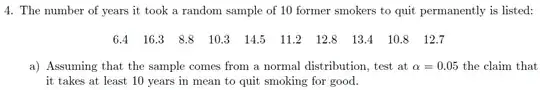It's possible to have undefined correlation -- what if one of the variables has zero standard deviation?
Consider for example
x 1 1 1 1
y 0 2 3 5
That said all those plots in your question have defined correlation... each of them is 0. Indeed, here's a new version of that plot which I generated randomly, with sample correlations (to the printed accuracy):
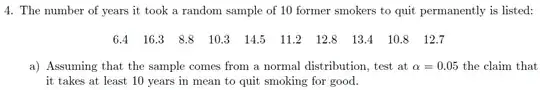
from comments:
Where in the calculations do we get zero in the numerator..? –
The numerator has a sum of products $\sum_i (x_i-\bar{x})(y_i-\bar{y})$. Each of those product-terms is a "deviation from horizontal mean, $\bar x$" times "deviation from vertical mean, $\bar y$. That contribution will be positive if both deviations have the same sign (both positive or both negative) and negative if they have opposite signs. Consider the signed area of a rectangle in these images representing contributions of such a product to the sum in the numerator:
(red for positive, blue for negative)
... representing the contributions of two points.
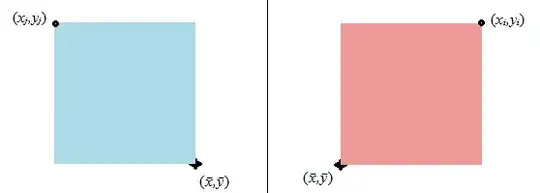
When the picture has left-to-right reflection-symmetry
then for each region in the plot contributing points like the one shaded red there's a corresponding region the opposite side of $\bar{x}$ contributing points like the one shaded blue (with perfect symmetry there will always be a pair of points that exactly cancel).
Similarly with top-to-bottom symmetry:
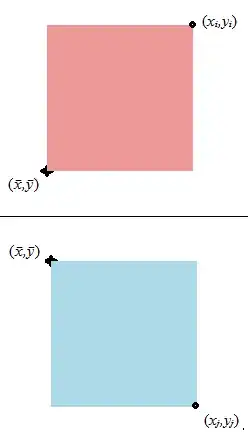
but this time there's a region as far the other side of $\bar{y}$.
As a result, any plot that shows reflective symmetry left to right or top to bottom will have a correlation-numerator of about 0 (or with perfect symmetry, of exactly 0). Every one of those five plots has left-to-right reflective symmetry and the last three have top-to-bottom symmetry as well. Consequently as long as neither variable has variance zero, the correlation will be zero. We can assess these symmetries with a mere glance and immediately and confidently conclude that they indicate no correlation.