I am curious about a normal distribution with no probability mass in certain regions, sort of like the complement of the truncated normal. In particular, it will have zero mass in a circular region.
Here is its pdf:
$$P(X | \mu, \Sigma) \propto I_{\{X \in C\}} exp\{-\frac{1}{2}(X - \mu)'\Sigma^{-1}(X - \mu)\}$$
Where $C$ is the set of all points that lie within the circle of interest, $I_{X \in C}$ is a function that takes value 1 when $X \in C$ and 0 otherwise (sometimes called the indicator function), $\mu$ is a mean vector, and $\Sigma$ is a positive definite covariance matrix.
Let me show some graphics illustrating what I mean.
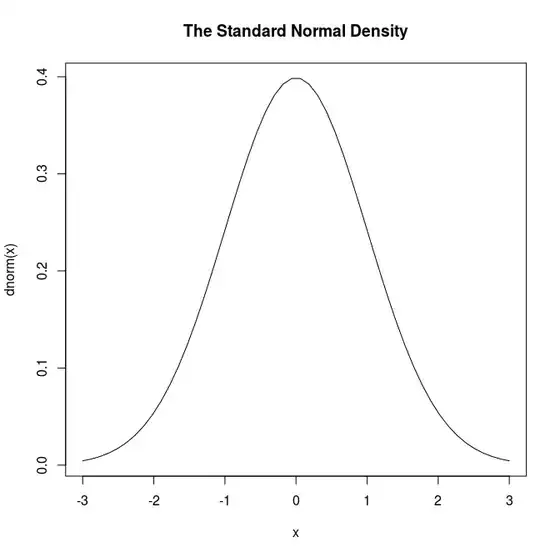
First in 1 dimension. This is the standard normal density:
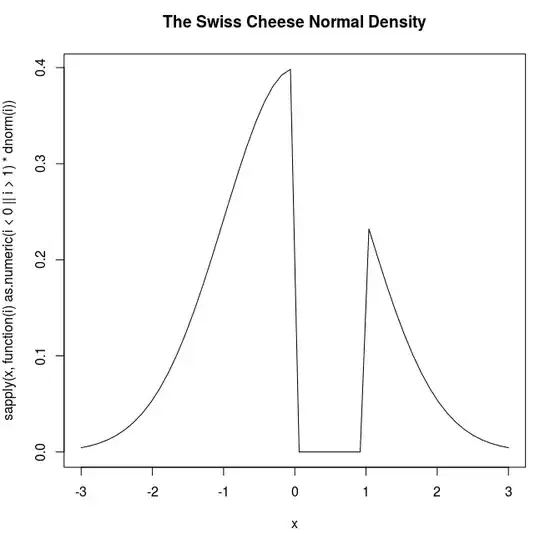
And now the swiss cheese density, with a circle centered at 0.5 with radius 0.5:
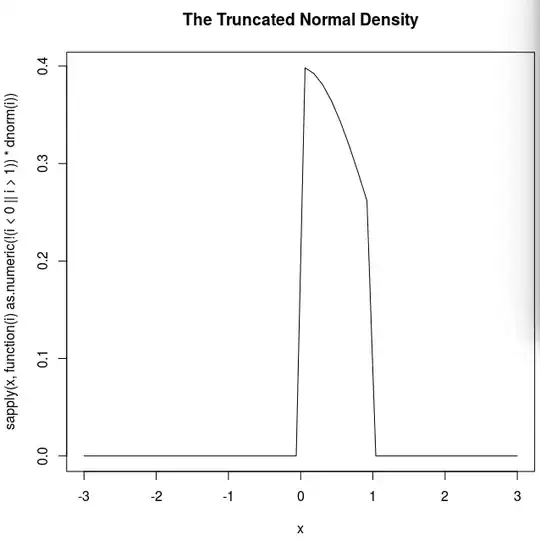
I would also like to contrast this with the truncated normal distribution over the same region:
(Notice that the y axis is incorrect on the last two charts as I have failed to renormalize this density; this is simply an illustrative tool)
In 1D, the Swiss Cheese distribution may be thought of as a mixture of truncated normal distributions. However, this is no longer the case in higher dimensions.
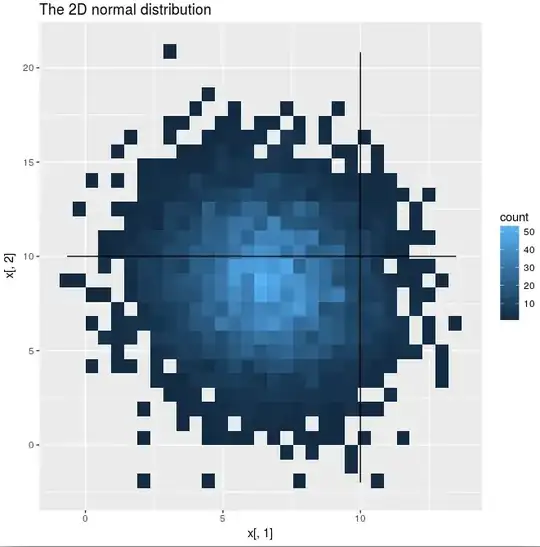
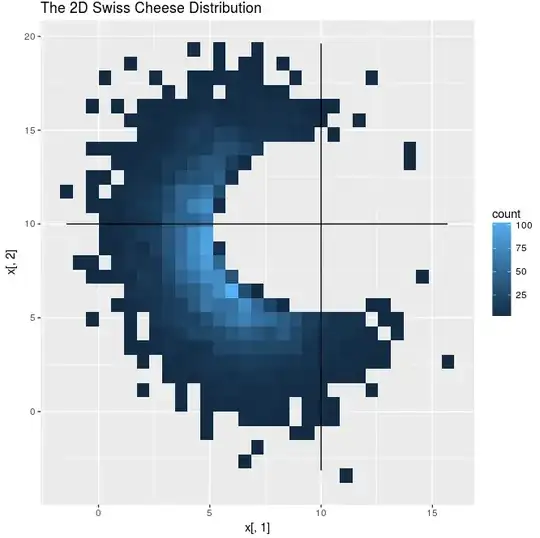
Let's consider a 2D case so that it may be visualized.
I will sample from a 2D gaussian and bin the results (since my ggplot skills are inadequate at best, I am unsure how to plot a 3D density):
And likewise for a 2D swiss cheese distribution:
I am interested in the higher D case, as well as the case where there are several circles cut out of the distribution.
Now my questions:
- Is there a name for such a distribution?
- Is there a source for results about such distributions?