2

Say I have two independent random variables $X \sim N(u_1, \sigma_1)$ and $Y \sim N(u_2, \sigma_2)$. I want to get the conditional distribution of X given whether X is bigger than Y or not.

$P(X|X<Y)$ = ... and

$P(X|X>Y)$ = ...

I am thinking solving this in this way:

\begin{align} P(X|X<Y) &= \frac{P(Y>X|X)P(X)}{P(Y>X)} \\ &= \frac{(1-\Phi(\frac{x-\mu_2}{\sigma_2}))N(\mu_1,\sigma_1)}{\Phi(\frac{\mu_2-\mu_1}{\sqrt{\sigma_2^2+\sigma_1^2}})}\\ P(X|X>Y) &= \frac{P(Y<X|X)P(X)}{P(Y<X)} \\ &= \frac{\Phi(\frac{x-\mu_2}{\sigma_2})N(\mu_1,\sigma_1)}{1-\Phi(\frac{\mu_2-\mu_1}{\sqrt{\sigma_2^2+\sigma_1^2}})} \end{align}

My questions are:

(1) Whether above solution is correct

(2) How to get the mean and sd for $P(X|X<Y)$ and $P(X|X>Y)$ if they are still normal?

HannaMao
  • 23
  • 7
  • What do you mean by "truncating" here? What happens to a draw of X if it's less than Y? It seems that you're using the term "truncate" not in its usual statistical meaning – Aksakal May 22 '17 at 15:14
  • I am sorry I may have used the wrong term. I would like to get the distribution of X if X < Y and the distribution of X if X> Y. I am wondering if there is any statistical formula can do this. – HannaMao May 22 '17 at 15:20
  • I thought the results would be a truncated normal distribution. – HannaMao May 22 '17 at 15:21
  • Although the procedure is related to truncation, the distribution function is not truncated. The integral to compute the distribution function of $X$ conditional on $Y\gt X$ is easily reduced to the one computed at https://stats.stackexchange.com/questions/61080. – whuber May 22 '17 at 16:44
  • @whuber If I understand correctly, the referred link calculated the joint distribution of [X, Y>X]. For my question, the conditional distribution should be the joint distribution divided by [Y>X]. Am I right? Thanks! – HannaMao May 22 '17 at 16:55
  • It computes the distribution function of $X$ conditional on an inequality. Of course it uses the joint distribution function to do that, but from what you have stated in your question it appears we are supposed to assume $X$ and $Y$ are independent, when your joint distribution is fully specified. – whuber May 22 '17 at 16:56

1 Answers1

1

Whether above solution is correct

Yes.

How to get the mean and sd for $P(X|X<Y)$ and $P(X|X>Y)$ if they are still normal?

They are not normal.

Proof:

Given $P(X | X>Y) = \frac{\Phi(\frac{x-\mu_2}{\sigma_2})\phi_x(\mu_1,\sigma_1)}{1-\Phi(\frac{\mu_2-\mu_1}{\sqrt{\sigma_2^2+\sigma_1^2}})}$ is equivalent to a product of a uniform random variable $(\Phi(\frac{x-\mu_2}{\sigma_2})$ and a normal random variable $(\phi_x(\mu_1,\sigma_1))$

Consider $X_1 \sim N(0, 1)$ and $X_2 \sim U(0,1)$, then the product $Z = X_1X_2$ distrobution is given by:

\begin{align*} F_Z(z) &= P(Z \leq z)\\ &= P(X_1X_2 \leq z)\\ &= \int_{X_1\geq 0}P(X_2 \leq \frac{z}{x_1}) \phi_{X_1}(x_1)\ dx_1 +\int_{X_1\leq 0}P(X_2 \geq \frac{z}{x_1}) \phi_{X_1}(x_1)\ dx_1\\ &= \int_{X_1\geq 0}\frac{z}{x_1} \phi_{X_1}(x_1)\ dx_1 + \int_{X_1\leq 0}(1-\frac{z}{x_1}) \phi_{X_1}(x_1)\ dx_1\\ &= \frac{1}{2} + \int_{X_1\geq 0}\frac{z}{x_1} \phi_{X_1}(x_1)\ dx_1 - \int_{X_1\leq 0}\frac{z}{x_1} \phi_{X_1}(x_1)\ dx_1 \\ &= \frac{1}{2} + \int\frac{2z}{x_1} \phi_{X_1}(x_1)\ dx_1 \end{align*}

which does not mimick CDF of a normal.

You can however still check if your solution is correct by simulation:

import matplotlib.pyplot as plt
import scipy as sp
import numpy as np

mu1 = 1
sigma1 = 2

mu2 = 2
sigma2 = 3

np.random.seed(42)
X = np.random.normal(mu1, sigma1, 1000)
Y = np.random.normal(mu2, sigma2, 1000)

# P(X|X>Y)
P_X_XgY = X[X>Y]
# P(X|X<Y)
P_X_XlY = X[X<Y]

denom = 1-sp.stats.norm.cdf((mu2-mu1)/np.sqrt(sigma1**2+sigma2**2))

count, bins, ignored = plt.hist(P_X_XgY, 30, normed=True)
plt.plot(bins, 1/(sigma1 * np.sqrt(2 * np.pi)) * \
(sp.stats.norm.cdf((bins-mu2)/sigma2)/denom) *\
np.exp( - (bins - mu1)**2 / (2 * sigma1**2) ), linewidth=2, color='r')
plt.title('$P(X|X>Y)$')

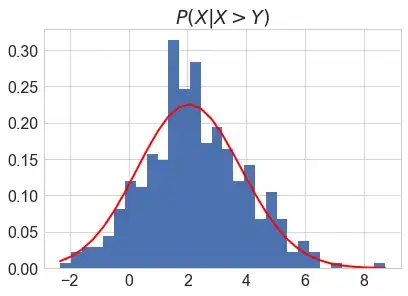
enter image description here

denom = sp.stats.norm.cdf((mu2-mu1)/np.sqrt(sigma1**2+sigma2**2))

count, bins, ignored = plt.hist(P_X_XlY, 30, normed=True)
plt.plot(bins, 1/(sigma1 * np.sqrt(2 * np.pi)) *\
((1-sp.stats.norm.cdf((bins-mu2)/sigma2))/denom) *\
np.exp( - (bins - mu1)**2 / (2 * sigma1**2) ), linewidth=2, color='r')
plt.title('$P(X|X<Y)$')

enter image description here

rightskewed
  • 3,040
  • 1
  • 14
  • 30
  • This is a wonderful answer! I am wondering if there is a name for the distribution of P(X|X>Y) or P(X|X – HannaMao May 23 '17 at 04:47
  • @whuber I am sorry I still couldn't get it. Here Z is the independent variable for $F_Z(z)$. I wanted it to be discussed more with x being the independent variable, $F_X(x)$. Did I make anything wrong? – HannaMao May 23 '17 at 15:34