I am trying to train a Deep Q Network (https://deepmind.com/research/dqn/) for a simple control task. The agent starts in the middle of a 1-dimensional line, at state 0.5. On each step, the agent can move left, move right, or stay put. The agent then receives a reward proportional to the absolute distance from its starting state. If the agent reaches state 0.35 or state 0.65, then the episode ends. So, effectively the agent is encouraged to move all the way to the left, or all the way to the right.
For now, I am just trying to train a deep neural network in Keras / Tensorflow, to predict the q-values of the three actions, in any given state. At each time step, actions are chosen randomly, so I am just trying to see if the network can predict the correct q-values, I am not trying to get the agent to actually solve the task. However, my network is struggling to learn the correct function.
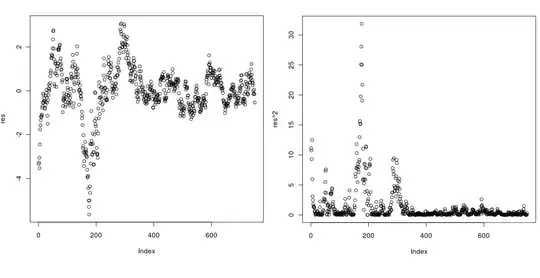
In this first figure below, the dots represent the training data available to the network on each weight update. These are stored in the experience replay buffer in the standard q-learning algorithm. As can be seen, states further from the centre have higher q-values, as would be expected. Also, when the state is greater than 0.5, higher q-values are assigned to the "move right" action, as would be expected, and vice versa. So, it seems that the training data is valid.
![1]](../../images/3793554497.webp)
In the next figure below, the predicted q-values are shown from my network. To get these values, I sampled uniformly from the range 0.35-0.65 to get the inputs, and then plotted the q-values for each action (the three coloured lines). The gradient is computed with respect to the difference between these predictions, and the training data in the first figure. So, these lines should match up to the points in the first figure. However, clearly they do not. They are predicting roughly the right values, but the shape of the lines are not consistent with the training data.
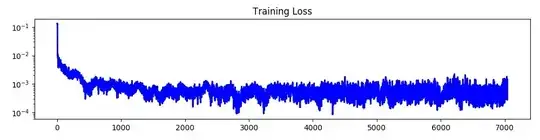
In the third figure below, I now plot the training loss for this network. So, it appears that training has converged, even though there is still significant error between the training data and the predictions. I am using mean squared error loss.
Finally, here are some details on my network itself. I use 1 layer of 16 hidden nodes, each with Relu activations, and the final layer has 3 nodes, one for each action. Although this is a simple network, it has enough capacity to learn the simple function in the first figure, from my prior experiments. I use the AdamOptimizer for optimisation, with a learning rate of 0.01, and I have also tried with a learning rate of 0.001 which also does not give the desired results. My batch size is 32. As with the standard Deep Q Network approach, I used a separate network for training the q values to the network used to predict the q values for the other states (as used in the Bellman equation).
So, I am puzzled as to what is going on. My network should be able to fit the training data, but it is not able to. I am not sure whether this is a problem with my optimisation, my network architecture, or my q learning algorithm. My intuition is that the learning rate is too low, because the predicted q values show a shape significantly different to the training q values, and so the network needs to be bumped significantly in the right direction. However, I am already using a learning rate of 0.01, which is very high.
Another thought I had is that the training error is pretty small (3 x 10^-4), and so it may not be possible to reduce this any more. Therefore, I would need to increase the size of the predicted q values (e.g. by increasing the scale of the reward), such that the absolute error is much larger, and therefore the optimiser can compute effective gradients. Does this make sense?
Any suggestions?