Quoting Weerahandi, Generalized Confidence Intervals (1993):
Confidence interval (Property 1) --- Consider a particular situation of interval estimation of a parameter $\theta$. If the same experiment is repeated a large number of times to obtain new sets of observations, then the $95\%$-confidence intervals will correctly include the true value of the parameter $\theta$ $95\%$ of the time.
Generalized confidence interval (Property 2) --- After a large number of independent situations of setting (generalized) $95\%$-confidence intervals for certain parameters of interest, the investigator will have correctly included the true values of the parameters in the corresponding intervals $95\%$ of the time.
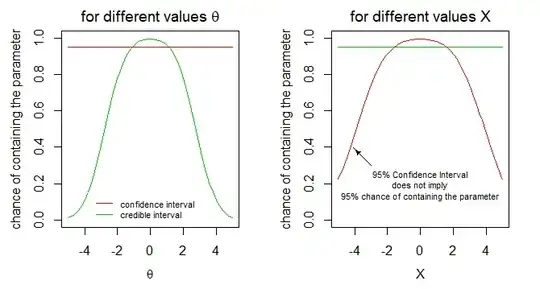
Property 1 implies Property 2.
This definition of a generalized confidence interval is not clear to me. Is there a mathematical, rigorous phrasing of Property 2? This is my main question.
I'm also not able to figure out what this property means in rigorous terms with the help of the mathematical construction of generalized confidence intervals (using generalized pivotal quantities). How can we "see" Property 2 from this construction?
It is also not clear to me why Property 2 does not imply Property 1. If the same expriment is repeated, these are not two "independent situations" in the sense of Property 2?
Note: It is known that Property 2 does not imply Property 1; a GCI is not a CI in general.
Edit
Theorem 2.1 of this paper gives more information. Its statement is the following one.
For every integer $k \geq 1$, let ${\cal M}_k$ be a statistical model with unknown parameter $\theta_k$. The ${\cal M}_k$'s have independent sample spaces.
Assume there are some observations for each ${\cal M}_k$ and denote by $I_k$ a corresponding generalized $95\%$-confidence interval.
Set $\delta_k=1$ if $\theta_k \in I_k$ and $\bar\delta_n = \frac{\sum_{k=1}^n\delta_k}{n}$. Then $\Pr(\lim_{n\to\infty}\bar\delta_n = 95\%)=1$. That is, as $n\to\infty$, the mean number of the GCIs $I_k$ containing $\theta_k$ tends to $95\%$ almost surely.