How is the cost function from Logistic Regression differentiated

Question

I am doing the Machine Learning Stanford course on Coursera.

In the chapter on Logistic Regression, the cost function is this:

Then, it is differentiated here:

I tried getting the derivative of the cost function, but I got something completely different.

How is the derivative obtained?

Which are the intermediary steps?

Answer 1

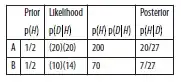
Adapted from the notes in the course, which I don't see available (including this derivation) outside the notes contributed by students within the page of Andrew Ng's Coursera Machine Learning course.

---

In what follows, the superscript $(i)$ denotes individual measurements or training "examples."

$\small \frac{\partial J(\theta)}{\partial \theta_j} = \frac{\partial}{\partial \theta_j} \,\frac{-1}{m}\sum_{i=1}^m \left[ y^{(i)}\log\left(h_\theta \left(x^{(i)}\right)\right) + (1 -y^{(i)})\log\left(1-h_\theta \left(x^{(i)}\right)\right)\right] \\[2ex]\small\underset{\text{linearity}}= \,\frac{-1}{m}\,\sum_{i=1}^m \left[ y^{(i)}\frac{\partial}{\partial \theta_j}\log\left(h_\theta \left(x^{(i)}\right)\right) + (1 -y^{(i)})\frac{\partial}{\partial \theta_j}\log\left(1-h_\theta \left(x^{(i)}\right)\right) \right] \\[2ex]\Tiny\underset{\text{chain rule}}= \,\frac{-1}{m}\,\sum_{i=1}^m \left[ y^{(i)}\frac{\frac{\partial}{\partial \theta_j}h_\theta \left(x^{(i)}\right)}{h_\theta\left(x^{(i)}\right)} + (1 -y^{(i)})\frac{\frac{\partial}{\partial \theta_j}\left(1-h_\theta \left(x^{(i)}\right)\right)}{1-h_\theta\left(x^{(i)}\right)} \right] \\[2ex]\small\underset{h_\theta(x)=\sigma\left(\theta^\top x\right)}=\,\frac{-1}{m}\,\sum_{i=1}^m \left[ y^{(i)}\frac{\frac{\partial}{\partial \theta_j}\sigma\left(\theta^\top x^{(i)}\right)}{h_\theta\left(x^{(i)}\right)} + (1 -y^{(i)})\frac{\frac{\partial}{\partial \theta_j}\left(1-\sigma\left(\theta^\top x^{(i)}\right)\right)}{1-h_\theta\left(x^{(i)}\right)} \right] \\[2ex]\Tiny\underset{\sigma'}=\frac{-1}{m}\,\sum_{i=1}^m \left[ y^{(i)}\, \frac{\sigma\left(\theta^\top x^{(i)}\right)\left(1-\sigma\left(\theta^\top x^{(i)}\right)\right)\frac{\partial}{\partial \theta_j}\left(\theta^\top x^{(i)}\right)}{h_\theta\left(x^{(i)}\right)} - (1 -y^{(i)})\,\frac{\sigma\left(\theta^\top x^{(i)}\right)\left(1-\sigma\left(\theta^\top x^{(i)}\right)\right)\frac{\partial}{\partial \theta_j}\left(\theta^\top x^{(i)}\right)}{1-h_\theta\left(x^{(i)}\right)} \right] \\[2ex]\small\underset{\sigma\left(\theta^\top x\right)=h_\theta(x)}= \,\frac{-1}{m}\,\sum_{i=1}^m \left[ y^{(i)}\frac{h_\theta\left( x^{(i)}\right)\left(1-h_\theta\left( x^{(i)}\right)\right)\frac{\partial}{\partial \theta_j}\left(\theta^\top x^{(i)}\right)}{h_\theta\left(x^{(i)}\right)} - (1 -y^{(i)})\frac{h_\theta\left( x^{(i)}\right)\left(1-h_\theta\left(x^{(i)}\right)\right)\frac{\partial}{\partial \theta_j}\left( \theta^\top x^{(i)}\right)}{1-h_\theta\left(x^{(i)}\right)} \right] \\[2ex]\small\underset{\frac{\partial}{\partial \theta_j}\left(\theta^\top x^{(i)}\right)=x_j^{(i)}}=\,\frac{-1}{m}\,\sum_{i=1}^m \left[y^{(i)}\left(1-h_\theta\left(x^{(i)}\right)\right)x_j^{(i)}- \left(1-y^{i}\right)\,h_\theta\left(x^{(i)}\right)x_j^{(i)} \right] \\[2ex]\small\underset{\text{distribute}}=\,\frac{-1}{m}\,\sum_{i=1}^m \left[y^{i}-y^{i}h_\theta\left(x^{(i)}\right)- h_\theta\left(x^{(i)}\right)+y^{(i)}h_\theta\left(x^{(i)}\right) \right]\,x_j^{(i)} \\[2ex]\small\underset{\text{cancel}}=\,\frac{-1}{m}\,\sum_{i=1}^m \left[y^{(i)}-h_\theta\left(x^{(i)}\right)\right]\,x_j^{(i)} \\[2ex]\small=\frac{1}{m}\sum_{i=1}^m\left[h_\theta\left(x^{(i)}\right)-y^{(i)}\right]\,x_j^{(i)} $

---

The derivative of the sigmoid function is

$\Tiny\begin{align}\frac{d}{dx}\sigma(x)&=\frac{d}{dx}\left(\frac{1}{1+e^{-x}}\right)\\[2ex] &=\frac{-(1+e^{-x})'}{(1+e^{-x})^2}\\[2ex] &=\frac{e^{-x}}{(1+e^{-x})^2}\\[2ex] &=\left(\frac{1}{1+e^{-x}}\right)\left(\frac{e^{-x}}{1+e^{-x}}\right)\\[2ex] &=\left(\frac{1}{1+e^{-x}}\right)\,\left(\frac{1+e^{-x}}{1+e^{-x}}-\frac{1}{1+e^{-x}}\right)\\[2ex] &=\sigma(x)\,\left(\frac{1+e^{-x}}{1+e^{-x}}-\sigma(x)\right)\\[2ex] &=\sigma(x)\,(1-\sigma(x)) \end{align}$

Answer 2

To avoid impression of excessive complexity of the matter, let us just see the structure of solution.

With simplification and some abuse of notation, let $G(\theta)$ be a term in sum of $J(\theta)$, and $h = 1/(1+e^{-z})$ is a function of $z(\theta)= x \theta $: $$ G = y \cdot \log(h)+(1-y)\cdot \log(1-h) $$

We may use chain rule: $\frac{d G}{d \theta}=\frac{d G}{d h}\frac{d h}{d z}\frac{d z}{d \theta}$ and solve it one by one ($x$ and $y$ are constants).

$$\frac{d G}{\partial h} = \frac{y} {h} - \frac{1-y}{1-h} = \frac{y - h}{h(1-h)} $$ For sigmoid $\frac{d h}{d z} = h (1-h) $ holds, which is just a denominator of the previous statement.

Finally, $\frac{d z}{d \theta} = x $.

Combining results all together gives sought-for expression: $$\frac{d G}{d \theta} = (y-h)x $$ Hope that helps.

Answer 3

The credit for this answer goes to Antoni Parellada from the comments, which I think deserves a more prominent place on this page (as it helped me out when many other answers did not). Also, this is not a full derivation but more of a clear statement of $\frac{\partial J(\theta)}{\partial \theta}$. (For full derivation, see the other answers).

$$\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m} \cdot X^T\big(\sigma(X\theta)-y\big)$$

where

\begin{equation} \begin{aligned} X \in \mathbb{R}^{m\times n} &= \text{Training example matrix} \\ \sigma(z) &= \frac{1}{1+e^{-z}} = \text{sigmoid function} = \text{logistic function} \\ \theta \in \mathbb{R}^{n} &= \text{weight row vector} \\ y &= \text{class/category/label corresponding to rows in X} \end{aligned} \end{equation}

Also, a Python implementation for those wanting to calculate the gradient of $J$ with respect to $\theta$.

import numpy
def sig(z):
return 1/(1+np.e**-(z))


def compute_grad(X, y, w):
    """
    Compute gradient of cross entropy function with sigmoidal probabilities

    Args: 
        X (numpy.ndarray): examples. Individuals in rows, features in columns
        y (numpy.ndarray): labels. Vector corresponding to rows in X
        w (numpy.ndarray): weight vector

    Returns: 
        numpy.ndarray 

    """
    m = X.shape[0]
    Z = w.dot(X.T)
    A = sig(Z)
    return  (-1/ m) * (X.T * (A - y)).sum(axis=1) 

Answer 4

For those of us who are not so strong at calculus, but would like to play around with adjusting the cost function and need to find a way to calculate derivatives... a short cut to re-learning calculus is this online tool to automatically provide the derivation, with step by step explanations of the rule.

https://www.derivative-calculator.net

Answer 5

Another presentation, with matrix notation.

Preparation: $\sigma(t)=\frac{1}{1+e^{-t}}$ has $\frac{d \ln \sigma(t)}{dt}=\sigma(-t)=1-\sigma(t)$ hence $\frac{d \sigma}{dt}=\sigma(1-\sigma)$ and hence $\frac{d \ln (1- \sigma)}{dt}=\sigma$.

We use the convention in which all vectors are column vectors. Let $X$ be the data matrix whose rows are the data points $x_i^T$. Using the convention that a scalar function applying to a vector is applied entry-wise, we have

$$mJ(\theta)=\sum_i -y_i \ln \sigma(x_i^T\theta)-(1-y_i) \ln (1-\sigma(x_i^T\theta))=-y^T \ln \sigma (X\theta)-(1^T-y^T)\ln(1-\sigma)(X\theta).$$

Now the derivative (Jacobian, row vector) of $J$ with respect to $ \theta$ is obtained by using chain rule and noting that for matrix $M$, column vector $v$ and $f$ acting entry-wise we have $D_v f(Mv)=\text{diag}(f'(Mv))M$. The computation is as follows:

$$m D_\theta J= -y^T [\text{diag}((1-\sigma)(X\theta))] X-(1^T-y^T) [\text{diag}(-\sigma(X\theta))]X=$$ $$=-y^TX+1^T[\text{diag}(\sigma(X\theta))]X=-y^TX+(\sigma(X\theta))^TX.$$

Finally, the gradient is

$$\nabla_\theta J=(D_\theta J)^T=\frac{1}{m}X^T(\sigma(X\theta)-y)$$