1

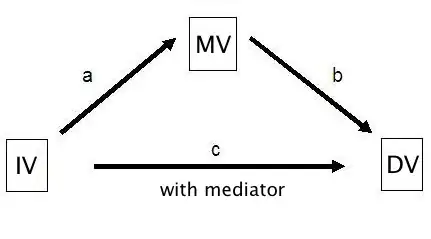
I am studying the effect of economic dissatisfaction on vote for the government at the individual level. I believe this relationship is partially mediated by attitudes towards the government record. The graph below presents the relationship I hypothesise, my IV is economic dissatisfaction (five points scale), my MV is approval of the government record (dichotomous) and my dependent variable is vote for the government (dichotomous).

enter image description here

Given that both the MV and the DV are binary measures, I calculate all three relationships/coefficients (a,b,c) with the use of logistic regressions.

My question is: how do I calculate the total effect (the unmediated plus the mediated parts) of the IV on the DV from the logistic regression coefficients?

I checked some of literature on mediated relationships and it seems to me that had this been a set of OLS regressions, one could use the following formula:

total effect of IV on DV = (a*b)+c

Is there a similar formula I could use based on the logit models?

Thank you!

Erdne Htábrob
  • 211
  • 2
  • 5
  • I think it is c, if your logistics regression on DV and IV does not include MV. – user158565 May 07 '17 at 10:05
  • $ab + c$ is the total effect on the log-odds, i.e. on your linear predictor. I see no problem in just reporting that. The effect of a unit increase in IV on logit$^{-1}(X\beta)$ will depend on where you start from because the logistic curve is non-linear. – Will May 07 '17 at 11:02
  • and to get to marginal effects, I could then just use something like **_exp(β)/(exp(β)+1)_**? – Erdne Htábrob May 07 '17 at 12:16
  • This is now a question about interpreting logistic regression coefficients. See [here](https://stats.stackexchange.com/questions/19764/marginal-effect-of-probit-and-logit-model) for a discussion of marginal effects in logistic regression. – Will May 07 '17 at 13:51
  • thank you for your help! if you write it up as an answer i am happy to accept it – Erdne Htábrob May 07 '17 at 13:55

1 Answers1

1

The formula You listed $a\cdot b+c$ works only for linear structural equations. If we consider generalized regression model then the relations are given by $\mathrm{MV}=f(d + a\cdot \mathrm{IV})$ and $\mathrm{DV}=g(e + c \cdot \mathrm{IV}+b\cdot\mathrm{MV})$ where $f$ and $g$ are functions.

The total effect of setting $\mathrm{IV}$ from value $u$ to value $w$ on $\mathrm{DV}$ is then given by (Pearl, 2009, p. 132):

$E[\mathrm{DV}_{\mathrm{IV}=w}-\mathrm{DV}_{\mathrm{IV}=u}]$, where $\mathrm{DV}_{\mathrm{IV}=x}=g(e + c \cdot x+b\cdot f(d + a\cdot x))$.

With $f$ and $g$ specified by logistic regression equation the equation for total effect can't be simplified. I suggest You estimate the total effect through simulation.

Pearl, J. (2009). Causality. Cambridge university press.

matus
  • 528
  • 3
  • 15
  • but what is in this equation e and d? and how would you do the simulations? Seems to me that this just got overly complex... can't I just do what Will suggested? – Erdne Htábrob May 07 '17 at 19:04
  • @EndreBorbáth feel free to use the linear equations, you just need to be aware that the computed coefficient doesn't correspond to the total effect and can't be interpreted causally. $e$ and $d$ are the regression offset parameters and I assume you include these in your logistic regression model irrespective of the question how to compute the total effect. In the linear case $e$ and $d$ are included in the computation as well, they just don't appear in the final formula. – matus May 07 '17 at 21:22
  • Suppose they are linear relation. Then DV=(e+bd) + (c+ba)IV. Why do not regress DV on IV directly to get the estimate of ab+c? I think this is kind of you create trouble for yourself when you drag MV into consideration. – user158565 May 07 '17 at 21:40
  • I am sorry to insist on this and I really appreciate your help but can I ask you to point me to some link or literature by what you mean by regression offset parameters? I tried to google this but all the hits seems to be related to Poisson models. Can this be the constant in each model or am I completely off? Thanks again! – Erdne Htábrob May 07 '17 at 21:40
  • @EndreBorbáth yeah, what I mean is the constant, also called intercept. Sorry for confusion. – matus May 07 '17 at 21:51
  • @a_statistician Yes, the two approaches (one regression vs two regressions) should provide the same result, if the relation is linear and Your suggested approach is simpler and hence preferable. – matus May 07 '17 at 22:04
  • i forgot to ask: is it the same formula if I want to know the confidence interval around the total effect? I just use the lower and upper bounds for the respective coefficients? – Erdne Htábrob May 08 '17 at 06:26
  • @EndreBorbáth I don't think that would work even in the linear case, since the estimate of lower and upper bounds may be correlated between $a$, $b$ and $c$ (even if the expected values are not). I would estimate the bounds through simulation, i.e. randomly generate values for $a$, $b$, $c$, fix $\mathrm{IV}$ to $w$ and $u$, randomly generate a large set of pairs $\mathrm{DV}_{\mathrm{IV}=w}$ and $\mathrm{DV}_{\mathrm{IV}=u}$, compute difference for each pair and the expectation across the set. Repeat for multiple values $a$, $b$ and $c$ to obtain set of values for tot. effect. – matus May 08 '17 at 10:36