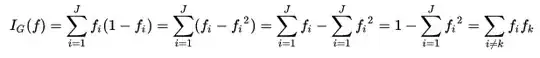Here is a snippet from my answer here. The easiest way (for me at least) to understand
$1-\sum f_i^2$ = $\sum_{i \neq k} f_if_k$
is by visually representing each of the elements in this equation. We'll assume that there are 4 labels below; however, this will scale to n values.

The value 1 is simply the sum of all possible probabilities. By definition this value must be 1.
The value $\sum f_i^2$ is the sum of probabilities of selecting a value and its label from the distribution of values.
Subtracting the probability that you match labels with values from 1 gives you the probability that you don't match labels and values. This is what the gini impurity provides -- the probability that you don't match labels to values.