3

Question :

A student bought 8 packets of crisps to eat and decided to weigh each packet. They discovered that 5 of them weighed less than the "average contents 25g" stated on the packet.

Is this significant at the 5% level?

Comment on the suitability of the test.

working

Assume that $P(x < \text{average}) = P(x > \text{average})$ for a packet.

This gives $p = 0.5$ , and $\hat{p} = \frac{5}{8} = 0.625$.

$\sigma = \sqrt{0.5 \times 0.5} = 0.5$

Standard error, $SE = \frac{\sigma}{\sqrt{n}} = \frac{0.5}{\sqrt{8}} \approx 0.177$

Using the above I have

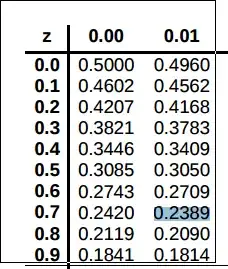
$z = \frac{\frac{5}{8} - \frac{1}{2}}{0.177} = \frac{\frac{1}{8}}{0.177} = 0.706 \approx 0.71$.

Looking up this value in the table gives

$z = 0.2389$

enter image description here

Which is not less than $0.05$, so we don't reject $H_0$ in this case (at a $5\%$ significance level)

The suitability of the test is questionable as the sample size is quite low. It's also not very clear what's meant by 'average' here.

binomial model

Using a binomial model instead of a $z$-test

I assume that $p = 0.5$, then I have $X \sim Bin(8, 0.5)$

To find whether the value of $\frac{5}{8}$ packets being underweight is significant (to a $95\%$ level) I use the model as

$$ P(X) = {n \choose x }p^x (1 - p)^{n - x} $$

As

$$ P(5) = {8 \choose 5}(0.5)^{5} (0.5)^{3} $$

Which gives $\frac{7}{32} = 0.21875$.

This is insignificant at a $5\%$ level.

The binomial test was more suitable for this situation as the values were low and easy to compute.

improvements

if the student had recorded the actual weight rather than just whether or not they were less than the given average then they would have been able to make inferences based on that data.

baxx
  • 738
  • 6
  • 21
  • 1
    Even assuming the binomial model is suitable, your binomial calculations are not the appropriate ones to test this hypothesis. You might want to review our posts on p-values, such as https://stats.stackexchange.com/questions/tagged/p-value?sort=votes&pageSize=50 – whuber Apr 26 '17 at 22:31
  • @whuber thanks - what's unsuitable about the binomial model here? It seems that I'm finding the probability of there being (5/8) , and from this I'm seeing whether it's 'particularly' unlikely or not. Here, particularly would be a value of 0.025 or less. – baxx Apr 26 '17 at 22:34
  • 1
    To appreciate the error, emulate your calculations with different numbers. Suppose, for instance, there were $1000$ packets and $501$ of them were underweight. (1) Intuitively, how strong is this evidence against the hypothesis that half or more of all packets meet the stated weight? (2) What number does your calculation give you? – whuber Apr 26 '17 at 22:36
  • @whuber cheers, `(1)` it's very weak evidence against the hypothesis, as it's only 'off by one' (where 1 is 1/1000). `(2)` my calculation is $P(X) = {1000 \choose x} p^{x}(1 - p)^{1000 - x}$ where $x = 501$, which gives roughly $0.0252$. Which isn't less than $0.025$ and isn't therefore evidence against the hypothesis. However, I think I see an error, as changing the values to `10,000` and `5001` I have a value which is `0.0079...`, but clearly this is **less** significant than that of the previous example (with 1000 and 501), so I'm interpreting the output wrong... – baxx Apr 26 '17 at 22:44
  • Am I just getting things flipped around, or am I going about the whole thing wrong? Thanks – baxx Apr 26 '17 at 22:44
  • 1
    You comment sounds thoroughly confused concerning what a p-value is and how to compute it. I will reiterate my recommendation to review the concepts of hypothesis testing and p-values. – whuber Apr 27 '17 at 13:14
  • @whuber thanks for the suggestion. The reasoning about 501/1000 being more "different" than 5001/10000 seems (though perhaps poorly written) sensical? There's a lot of links from what you suggested (which may all be needed, but I don't currently have time for all). If there's nothing more specific you suggest I'll look at this answer https://stats.stackexchange.com/a/130772/137921 , which looks interesting. Cheers – baxx Apr 27 '17 at 13:22
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/57836/discussion-between-baxx-and-whuber). – baxx Apr 27 '17 at 14:52

1 Answers1

2

Don't worry about what exactly "average" means in the question because you're given no information about how it was computed; it can only really serve as a benchmark value.

You have dichotomous data. A binomial test is a better fit for this than a $z$-test. I believe the part that says "Comment on the suitability of the test" is hinting that if you were the student, there's a better way to collect the data that would allow you to conduct a more powerful test.

Kodiologist
  • 19,063
  • 2
  • 36
  • 68
  • thanks - I've updated the OP with the binomial test. I'm not sure what a better approach to data collection would be though? (other than just getting loads more samples) – baxx Apr 26 '17 at 22:29
  • 1
    @baxx The student recorded whether each packet weighed more or less than 25g, but not its actual weight. – Kodiologist Apr 26 '17 at 22:49
  • Oh , of course. So if they had recorded the weight of the packets then instead of a binomial model they would have been able to find the mean of the sample - *then* a $z$-test would have been more appropriate? – baxx Apr 26 '17 at 23:02
  • 1
    @baxx Right. (>'-')> – Kodiologist Apr 27 '17 at 02:34
  • cheers, is my use of the binomial model incorrect in the edit that I made? – baxx Apr 27 '17 at 09:13
  • 1
    @baxx Yes, in R, `binom.test(5, 8)` yields .727, whereas you got .219. – Kodiologist Apr 27 '17 at 14:27
  • @baxx Look again, I typed in the wrong value. – Kodiologist Apr 27 '17 at 14:29
  • ah right. well i have no idea then, currently trying to understand one of the other threads I was linked to by someone else :S – baxx Apr 27 '17 at 14:30