In Reinforcement learning, learning without the need for the transition probability matrix is 'model free learning'. Instead of having the transition probabilities, we learn the q-values (state/action functions), eventually getting the optimal strategy.
Why there is no transition probability in Q-Learning (reinforcement learning)?
Is it possible at all to make a transition probability matrix using the normalized Q values?
No, it is not possible. Why? Because the Q-values don't tell you anything about where you will end up when you are in state $s$ and take action $a$. $Q^\pi(s, a)$ is the expected discounted reward of being in state $s$, taking action $a$ and following policy $\pi$ thereafter.
Example
Let's say we have a small gridworld as an environment and we can interact with it.
States: $\{\texttt{NW}, \texttt{N}, \texttt{NE}, \texttt{W}, \texttt{C}, \texttt{E}, \texttt{SW}, \texttt{S}, \texttt{SE}\}$.
(Northwest, North, Northeast, West, Center, East, Southwest, South and Southeast)
Actions: $\{\texttt{U}, \texttt{D}, \texttt{L}, \texttt{R}\}$
(Up, Down, Left, Right)
After interacting with the environment using a model-free algorithm (e.g. Q-learning, SARSA) you obtain the optimal Q-values.
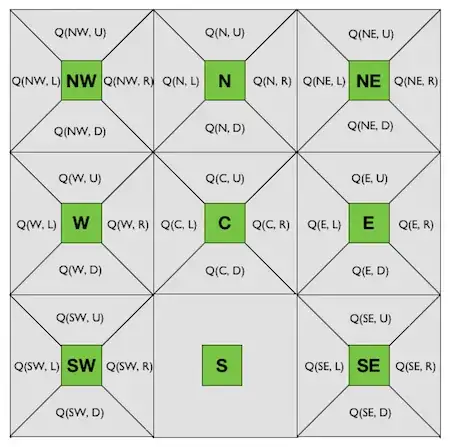
As we know the transition function, $T(s, a, s')$, gives us the probability that when we are in state $s$ and take action $a$, we end up in next state $s'$.
By looking at this gridworld it is intuitive to assume that if we are in state $\texttt{C}$ and take action $\texttt{D}$ we end up in in $\texttt{S}$, i.e., $T(\texttt{C}, \texttt{D}, \texttt{S}) = 1$. But we don't know that. We would be just assuming a transition function. What if 50% of the time we are in state $\texttt{C}$ and take action $\texttt{D}$ we end up in in state $\texttt{W}$ and the other 50% in state $\texttt{S}$, i.e., $T(\texttt{C}, \texttt{D}, \texttt{W}) = 0.5$, $T(\texttt{C}, \texttt{D}, \texttt{S}) = 0.5$?
Now, let's say that the Q-values for state $\texttt{C}$ are:
Those Q-values don't tell us anything with respect to the transition function. Is just telling us that taking action $\texttt{D}$ gives us the best discounted reward if we follow the optimal policy after that. But we don't know where it would take us.
However, you can learn the transition and reward functions using something like Sutton's Dyna architecture.
